1. (Dificultad: 5/10) Calcule el siguiente límite:
$$ \lim_{x \to -\infty} \frac{\sqrt{x^2-1}}{2x+1} $$
SOLUCIÓN
Proposición |
Razón |
|
| 1. | $$ \lim_{x \to -\infty} \frac{\sqrt{x^2-1}}{2x+1} $$ | Planteamiento |
| 2. | $$ \lim_{x \to -\infty} \frac{\sqrt{x^2 \left( 1-\frac{1}{x^2} \right)}}{x(2+\frac{1}{x})} $$ | Factores comunes. |
| 3. | $$ \lim_{x \to -\infty} \frac{\sqrt{x^2} \sqrt{1-\frac{1}{x^2}}}{x(2+\frac{1}{x})} $$ | Propiedad de radicales. |
| 4. | $$ \lim_{x \to -\infty} \frac{\left| x \right| \sqrt{1-\frac{1}{x^2}}}{x(2+\frac{1}{x})} $$ | De 3. Aplico la ecuación \( \sqrt{x^2} = \left| x \right| \). Cierta para todos los valores de \(x\). Ver texto de cálculo de Stewart, edición 8, página A7, en español. |
| 5. | $$ \left| x \right|=-x~\text{si}~x<0 $$ | Tenemos en cuenta parte de la definición de la función valor absoluto. Esto se cumple dado que el límite tiende a menos infinito. |
| 6. | $$ \lim_{x \to -\infty} \frac{-x \sqrt{1-\frac{1}{x^2}}}{x(2+\frac{1}{x})} $$ | Sustitución de 5 en 4. |
| 7. | $$ \lim_{x \to -\infty} -\frac{ \sqrt{1-\frac{1}{x^2}}}{2+\frac{1}{x}} $$ | Se opera \(x\) en numerador y denominador. |
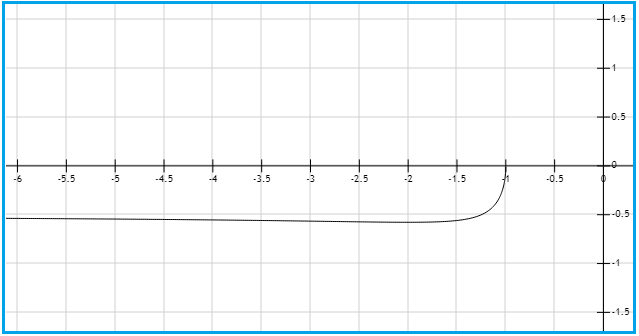
| 8. | $$ -\frac{\sqrt{1-0}}{2+0} = - \frac{1}{2} $$ | Se calcula el límite. El operador ingresa dentro de la raiz cuadrada y, sabiendo que el límite cuando x tiende a infinito, o menos infinito, de la forma 1/(x^r) es igual a cero. |




Comentarios potenciados por CComment