4. (Dificultad: 4/10) Calcule el siguiente límite, si existe:
$$ \lim_{x \to -\infty} \frac{\left| x \right|}{3 \left| x \right| + 5} $$
Solución
Proposición |
Razón |
|
| 1. | $$ \lim_{x \to -\infty} \frac{\left| x \right|}{3 \left| x \right| + 5} $$ | Planteamiento del problema |
| 2. | $$ \left| x \right| = -x~\text{si}~x<0 $$ | Parte de la definición de la función valor absoluto. Se cumple, dado que el límite tiende a un valor negativo muy grande. |
| 3. | $$ \lim_{x \to -\infty} \frac{ -x }{-3x + 5} $$ | Sustitución de 2 en 1. |
| 4. | $$ \lim_{x \to -\infty} \frac{ -\frac{x}{x} }{ \frac{-3x}{x} + \frac{5}{x} } $$ | De 3. Divido numerador y denominador por la mayor potencia de x del denominador. |
| 5. | $$ \lim_{x \to -\infty} \frac{ -1 }{ -3 + \frac{5}{x} } $$ | De 4. Propiedad de los reales. |
| 6. | $$ \frac{-1}{-3+0} = \frac{1}{3} $$ | Se tiene en cuenta que el límite cuando x tiende a menos infinito de 5/x es igual a cero. |
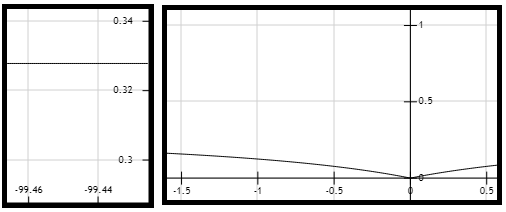
Figura 1. Gráficas de la función \( f(x)=\frac{\left| x \right|}{3 \left| x \right| + 5} \).




Comentarios potenciados por CComment