Solución

	Proposición	Razón
1.	$$ \lim_{x \to 0} \frac{\ln{\cos (2x)}}{7x^2} $$	Planteamiento
2.	$$ \rightarrow \frac{0}{0} $$	El cálculo del límite presenta la forma indeterminada cero sobre cero, dado que el coseno de cero es igual a uno y el logaritmo natural de uno es igual a cero. Se procede a aplicar la regla de L'Hopital derivando numerador y denominador.
3.	$$ \lim_{x \to 0} \frac{\frac{-2 \sin{2x}}{\cos{2x}}}{14x} $$	De 1. Se aplicó regla de L'Hopital.
4.	$$ \lim_{x \to 0} - \frac{\sin{2x}}{7x \cos{2x}} \rightarrow \frac{0}{0} $$	De 3. Se aplican propiedades de las fracciones y se reorganiza. Si se evalúa el límite se obtiene nuevamente la forma indeterminada cero sobre cero. Se aplicará nuevamente la regla de L'Hopital.
5.	$$ \lim_{x \to 0} - \frac{2 \cos{2x}}{7 \left[ x (-\sin{2x})(2) + \cos{2x}(1) \right]} $$	De 4. Se aplicó regla de L'Hopital. En el numerador se tiene la derivada de un producto.
6.	$$ - \frac{2 \cos{0}}{7 \left[ (0) (-\sin{0})(2) + \cos{0}(1) \right]} = - \frac{2}{7} $$	De 5. Se evalúa el límite y se resuelve.

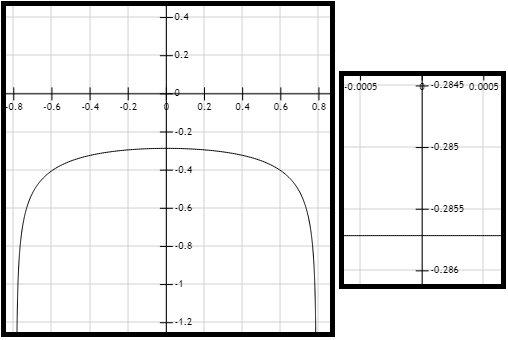
Figura 1. Gráfica de la función $y=\frac{\ln{\cos (2x)}}{7x^2} $.

Comentarios potenciados por CComment

Ejercicio resuelto 6 | Límites con regla de L'Hopital