Ejercicios de cálculo diferencial

1. (Dificultad: 6/10) Una lámpara está instalada en lo alto de un poste de 6 m de altura. Un hombre de 2 m de estatura se aleja caminando desde el poste con una rapidez de 1.5 m/s a lo largo de una trayectoria rectilínea. ¿Qué tan rápido se desplaza la punta de su sombra cuando el hombre está a 10 m del poste?

Solución

Primero se define la lámpara como el punto B, siendo el poste el segmento AB. El hombre está representado por el segmento ED. La punta de la sombra es el punto C. Para resolver el problema se puede usar la semejanza que existe entre los triángulos \(\triangle ABC\) y \(\triangle EDC\). Los dos triángulos son semejantes dado que tienen la misma forma. Para más detalles en relación con el tema de semejanza de triángulos se remite al lector a la sección de Geometría, en donde hallará problemas en donde se demuestra la semejanza entre triángulos. También es necesario definir a \(L\) como la distancia del hombre al poste en cualquier instante de tiempo y a la distancia \(x\) como la distancia de la punta de la sombra en cualquier instante de tiempo.

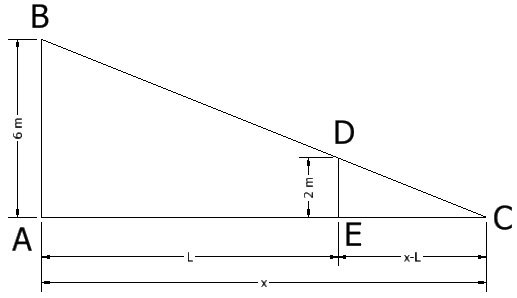
 Al tener la semejanza entre los triángulos \(\triangle ABC\) y \(\triangle EDC\) se pueden aprovechar las proporciones que se pueden forman a partir de la semejanza y escribir:

$$ \frac{x}{x-L} = \frac{6~m}{2~m} $$

De donde se obtiene:

$$ \frac{x}{x-L} = 3 $$

Se pone \(x\) en función de \(L\), así:

$$ x = 3x - 3L $$

$$ 3L = 3x-x $$

$$ 3L = 2x $$

Finalmente, se obtiene una expresión para la distancia de la punta de la sombra \(x\) en función de la distancia del hombre al poste \(L\):

$$ x = \frac{3}{2} L $$

A continuación se deriva implícitamente con respecto al tiempo la expresión anterior y se obtiene:

$$ \frac{dx}{dt} = \frac{3}{2} \frac{dL}{dt} $$

Si el problema nos dice que el hombre camina a una velocidad de 1.5 m/s, entonces:

$$ \frac{dL}{dt} = 1.5~m/s $$

Sustituyendo este valor en la expresión para \(dx/dt\):

$$ \frac{dx}{dt} = \frac{3}{2} \left( 1.5~m/s \right) $$

$$ \frac{dx}{dt} = \frac{3}{2} \left( \frac{3}{2}~m/s \right) $$

Finalmente, la respuesta es:

$$ \frac{dx}{dt} = \frac{9}{4}~m/s $$

Nótese que el problema pregunta por la velocidad a la que la punta de la sombra se aleja del poste cuando el hombre está a 10 metros de éste, sin embargo, se acaba de encontrar que dicha velocidad no es función de la distancia del hombre al poste, sino sólo de la velocidad a la cual el hombre camina con respecto al poste.