Ejercicios de vectores - thefinitelement.com

: Última actualización: 03 Abril 2023; Visto: 14020

1. Considere los siguientes puntos del plano con coordenadas:

$$P_1(2,1),~Q_1(3,3),~P_2(4,-2),~Q_2(2,-3),~P_3(-3,-1),~Q_3(0,-2)$$

Considere también los vectores $\overrightarrow{u}=\overrightarrow{P_1 Q_1}$, $\overrightarrow{v}=\overrightarrow{P_2 Q_2}$ y $\overrightarrow{w}=\overrightarrow{P_3 Q_3}$. Calcular:

a. El vector $\overrightarrow{u}-2\overrightarrow{v}+\overrightarrow{w}$.

b. La magnitud del vector $\overrightarrow{w}$, $\|w\|$.

c. Los ángulos entre los vectores $\overrightarrow{u},~\overrightarrow{v}$ y entre los vectores $\overrightarrow{u},~\overrightarrow{w}$.

d. $Proy_{\overrightarrow{v}} (\overrightarrow{u})$ y $Proy_{\overrightarrow{w}} (\overrightarrow{u})$.

Respuestas:

a. (8,3).

b. $\sqrt{10}$.

c. 143.1$^\circ$, 81.2$^\circ$.

d. $\frac{4}{5}(2,1)$, $\frac{1}{10}(3,-1)$.

2. Pruebe que los triángulos con vértices A(-3,2), B(1,0), C(4,6) y F(1,1,-1), G(-3,2,-2), H(2,2,-4) son triángulos rectángulos.

3. Halle todos los valores del escalar $k$ para los cuales los dos vectores siguientes son ortogonales.

$$ \overrightarrow{u} = (1,-1,2) $$

$$ \overrightarrow{v} = (k^2,k,-3) $$

Resp: -2, 3.

4. Sean $\overrightarrow{V}=(1,-1,0)$ y $\overrightarrow{W}=(1,1,0)$. Encontrar las coordenadas de un vector $\overrightarrow{U}$ de $R^3$ que cumpla simultáneamente con $\overrightarrow{U} \perp \overrightarrow{V}$, $\| \overrightarrow{U} \| = 4$ y que el ángulo entre $\overrightarrow{U}$ y $\overrightarrow{W}$ sea igual a $\pi/3$.

Solución: Solución de ejercicio 4 - Geometría Vectorial.

5. Se tienen dos vectores $A=\langle 2,-1,2 \rangle$ y $B=\langle 1,2,-3 \rangle$. Hallar los vectores $\overrightarrow{C}$ y $\overrightarrow{D}$ en $\mathbb{R}^3$, tal que $\overrightarrow{A}=\overrightarrow{C}+\overrightarrow{D}$, $\overrightarrow{B} \cdot \overrightarrow{D}=0$ y $\overrightarrow{C}$ paralelo a $\overrightarrow{B}$.

Solución: Geometría vectorial | Ejercicio 5 | Vectores perpendiculares y paralelos

6. Compruebe que $ (\overrightarrow{u}+\overrightarrow{v}) \cdot (\overrightarrow{u}-\overrightarrow{v}) = \|\overrightarrow{u}\|^2 - \|\overrightarrow{v}\|^2 $ para vectores $\overrightarrow{u}$ y $\overrightarrow{v}$ cualquiera. Aquí el punto representa el producto punto o producto escalar.

7. Dados $\overrightarrow{u}=5\hat{i}+12\hat{j}$ y $\overrightarrow{v}=\hat{i}+k\hat{j}$, donde $k$ es un escalar, encuentre $k$ de tal manera que la medida en radianes del ángulo entre $\overrightarrow{u}$ y $\overrightarrow{v}$ sea $\frac{\pi}{3}$. Respuesta:

$$ \frac{-240+\sqrt{85,683}}{407} $$

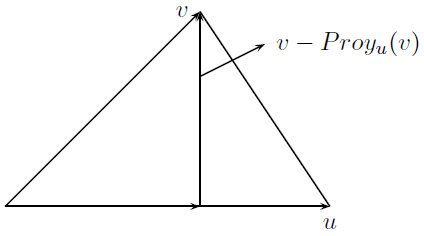
8. A partir del dibujo que se muestra a continuación, demostrar que el área $A$ de un triángulo se puede calcular como:

$$ A=\frac{\|\overrightarrow{u}\|~\|\overrightarrow{v}-Proy_{\overrightarrow{u}} (\overrightarrow{v})\|}{2} $$

9. Calcule el área del triángulo cuyos vértices son A(1,-1), B(2,2), C(4,0). Respuesta: 4.

10. Usando la expresión para calcular la proyección de un vector sobre otro, demuestre que la distancia de un punto $P(x_1,y_1)$ a la recta $Ax+By+C=0$ está dada por:

$$ d=\frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}} $$

Solución: Ejercicio resuelto 10 | Geometría vectorial

11. Se tiene un triángulo $\triangle ABC$ cuyos vértices son $A(3,-3,1)$, $B(0,1,3)$ y $C(-1,3,2)$. Use métodos vectoriales para hallar el pie de la altura relativa al lado $BC$ del $\triangle ABC$.

12. Hallar el área del triángulo cuyos vértices son los puntos: $A(1,1,3)$, $B(2,-1,5)$, $C(-3,3,1)$ utilizando solo proyecciones vectoriales.

13. Sean los vectores $\overrightarrow{a}=(-1,5,7)$ y $\overrightarrow{e}=(1,-2,3)$, descomponga $\overrightarrow{a}$ en la suma de dos vectores libres $\overrightarrow{x}$ y $\overrightarrow{y}$, tales que $\overrightarrow{x}$ sea paralelo a $\overrightarrow{e}$ y $\overrightarrow{y}$ sea ortogonal a $\overrightarrow{e}$. Hallar los vectores $\overrightarrow{x}$ y $\overrightarrow{y}$. Solución de ejercicio 13 | Geometría Vectorial

14. Se tiene el triángulo $\triangle ABC$ con vértices $A(4,2,0)$, $B(3,4,-3)$ y $C(7,0,1)$. Empleando procedimientos vectoriales:

a) Demostrar que el triángulo es isósceles.

b) Demostrar que la mediana relativa a la base es también perpendicular a ella.

c) Hallar el área del triángulo.

Solución: Solución de ejercicio 14 | Geometría Vectorial

15. Sean $\overrightarrow{V}=(3,1,0)$ y $\overrightarrow{W}=(2,2,0)$. Encontrar las coordenadas de un vector $\overrightarrow{U}$ de $R^3$ que cumpla simultáneamente las dos condiciones siguientes.

a) $\overrightarrow{U} \perp \overrightarrow{W}$.

b) $Proy_{\overrightarrow{V}}\overrightarrow{U} =-2 \overrightarrow{V}$.

Solución: Ejercicio resuelto 15 | Geometría vectorial

16. Sean $\overrightarrow{U}$, $\overrightarrow{V}$ y $\overrightarrow{W}$ vectores en $R^2$ tales que $\|\overrightarrow{U}\|=3$, $\|\overrightarrow{V}\|=4$ y $\|\overrightarrow{W}\|=2$. Si el ángulo entre $\overrightarrow{U}$ y $\overrightarrow{V}$ es de $60°$, el ángulo entre $\overrightarrow{V}$ y $\overrightarrow{W}$ es de $120°$, y si $\overrightarrow{Z}=2 \overrightarrow{U} - \overrightarrow{V}+3\overrightarrow{W}$, calcular $\overrightarrow{Z} \cdot \overrightarrow{V}$.

Solución: Ejercicio resuelto 16 | Geometría vectorial

17. Calcular las coordenadas del baricentro del triángulo con vértices $A(3,1)$, $B(6,7)$ y $C(-2,8)$.

Solución: Ejercicio resuelto 17 | Geometría vectorial

18. Hallar un vector $\overrightarrow{A}$ en la misma dirección del vector $\overrightarrow{B}=\hat{i}-2\hat{j}+3\hat{k}$ que determine con el vector $\overrightarrow{w}=-2\hat{i}+4\hat{j}-\hat{k}$ un paralelogramo de área 25 unidades cuadradas.

Solución: Ejercicio resuelto 18 | Area de un paralelogramo en R3

19. Sean $\overrightarrow{u}$ y $\overrightarrow{v}$ vectores de $R^3$ y $\theta$ el ángulo entre $\overrightarrow{u}$ y $\overrightarrow{v}$. Demuestre que el área del triángulo determinado por ambos vectores es:

$$ \frac{\| u \times v \|}{2} $$

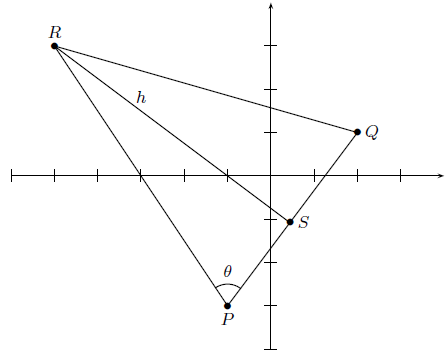
20. Considere el triángulo que se presenta en la siguiente figura, cuyos vértices se encuentran en los puntos de coordenadas $P(-1,-3)$, $Q(2,1)$, $R(-5,3)$.