Viscosidad Ejercicio 1

Visto: 3889

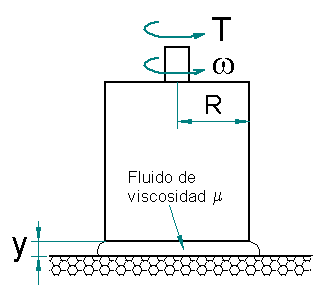
Se tiene un cilindro sobre una superficie como se ve en la Figura 1. Entre la superficie y el cilindro hay una capa de líquido con viscosidad

\[ \mu \]
y dicho cilindro gira a una velocidad angular constante
\[ \omega \]
determinada. La separación entre el cilindro y la superficie es "y", y el radio del cilindro es constante e igual a R.

 

Figura 1.

1. Aplicando la ecuación para el esfuerzo cortante, halle una expresión para hallar el torque T que se debe aplicar para mantener el cilindro girando. La expresión debe estar en función de

\[ \mu \]
, R,
\[ \omega \]
e y.

2. Teniendo en cuenta la expresión hallada para T, deduzca una para hallar la viscosidad

\[ \mu \]
.

Desarrollo

1. La expresión para el esfuerzo cortante es:

\[ \tau = \mu \frac{du}{dy} \]

Luego, tenemos que el esfuerzo es igual a un diferencial de fuerza sobre un diferencial de área,

\[ \frac{dF}{dA} = \mu \frac{du}{dy} \]

De donde,

\[ dF = \mu \frac{du}{dy} dA \]

Luego, al ser una distancia de separación pequeña podemos hacer,

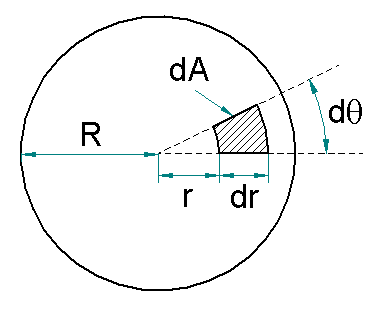
\[ \frac{du}{dy} = \frac{\Delta u}{\Delta y} = \frac{\omega r - 0}{y - 0} = \frac{\omega r}{y} \]

Al tener en cuenta el análisis diferencial expuesto en la Figura 2 deducimos que,

\[ dA = r~dr~d\theta \]

Figura 2. Análisis diferencial de la superficie del fondo del cilindro.

 Reemplazando los valores de dA y du/dy en dF resulta,

\[ dF = \frac{\mu \omega}{y} r^2 dr d\theta \]

Para hallar el torque necesitamos la ecuación diferencial para el torque, la cual es,

\[ dT = dF.r = \frac{\mu \omega}{y} r^3 dr d\theta \]

Integrando para hallar el valor de T,

\[ T = \int_0^T dT = \frac{\mu \omega}{y} \int_0^{2\pi} \int_0^R r^3 dr~d\theta \]

Finalmente,

\[ \boxed{T = \frac{\pi \mu \omega R^4}{2y}} \]

2. Como ya se tenía la expresión para el torque solo despejamos la viscosidad para dejarla en función del torque, la velocidad angular, la separación y el radio del cilindro, así:

\[ \boxed{\mu = \frac{2yT}{\pi \omega R^4}} \]

Comentarios potenciados por CComment