Viscosidad Ejercicio 2

Visto: 2501

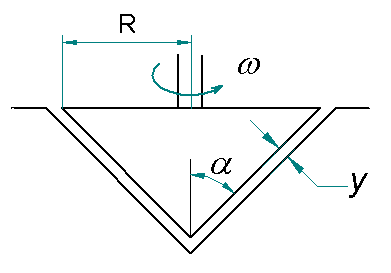
Calcular el momento torsional necesario para hacer girar el cono mostrado en la Figura 1 a una velocidad ω constante si un fluido de viscosidad μ llena el espacio entre él y la superficie cónica. Dicha separación tiene un valor de "y", el radio del cono es R y el ángulo que forma la pared con la vertical es α.

 

Figura 1.

Desarrollo

1. La expresión para el esfuerzo cortante es:

\[ \tau = \mu \frac{du}{dy} \]

Luego, tenemos que el esfuerzo es igual a un diferencial de fuerza sobre un diferencial de área,

\[ \frac{dF}{dA} = \mu \frac{du}{dy} \]

Debido a que la separación entre las superficies es muy pequeña podemos decir que,

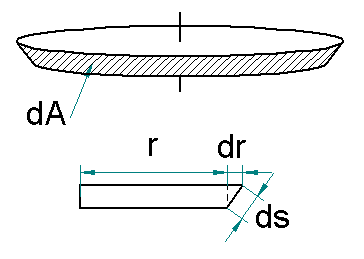
\[ \frac{du}{dy}=\frac{\Delta u}{\Delta y} = \frac{\omega . r - 0}{y-0} = \frac{\omega . r}{y} \]

Ahora, tomando el diferencial de área aproximadamente como una cinta cónica, como se aprecia en la Figura 2, decimos que,

\[ dA = 2 \pi r ~ds = 2 \pi r \frac{dr}{\sin \alpha} \]

Figura 2. Tomando el diferencial de área.

Sabiendo de antemano que,

\[ \sin \alpha = \frac{dr}{ds} \]

Luego, tenemos la expresión para dF al reemplazar du/dy y dA.

\[ dF = \frac{2 \pi \mu \omega}{y \sin \alpha} r^2~dr \]

Tomando la ecuación diferencial para el torque tendremos,

\[ dT = dF~r= \frac{2 \pi \mu \omega}{y \sin \alpha} r^3~dr \]

\[ T = \frac{2 \pi \mu \omega}{y \sin \alpha} \int_0^R r^3~dr \]

Finalmente, luego de haber integrado dT entre 0 y T y el radio entre 0 y R resulta,

 

\[ \boxed{T = \frac{\pi \mu \omega r^4}{2 y \sin \alpha}} \]

Comentarios potenciados por CComment