1. (Dificultad: 6/10) Resolver para \(x\).
$$ \frac{1}{\log_{x^3}10}-24 \log_{x^2}10+5=0 $$
Recomendación: pasar a base 10.
SOLUCIÓN
Proposición |
Razón |
|
| 1. | $$ \frac{1}{\log_{x^3}10}-24 \log_{x^2}10+5=0 $$ | Planteamiento del problema. |
| 2. | $$ \frac{1}{\log_{x^3}10}=24 \log_{x^2}10-5 $$ | Propiedad de los reales. |
| 3. | $$ \log_a b=\frac{\log_c b}{\log_c a} $$ | Formula para cambio de base. |
| 4. | $$ \log_{x^2} 10=\frac{\log_{10} 10}{\log_{10} x^2}=\frac{1}{2 \log_{10} x} $$ | De 3 y 2. Cambio de base. |
| 5. | $$ \log_{x^3} 10=\frac{\log_{10} 10}{\log_{10} x^3}=\frac{1}{3 \log_{10} x} $$ | De 3 y 2. Cambio de base. |
| 6. | $$ \frac{1}{ \frac{1}{3 \log_{10} x } } = 24 \left( \frac{1}{ 2\log_{10} x } \right) - 5 $$ | Sustitución de 4 y 5 en 2. |
| 7. | $$ 3 \log_{10} x + 5 = 12 \left( \frac{1}{\log_{10} x} \right) $$ | Opero fracción a la izquierda y propiedad de los reales. |
| 8. | $$ 3 \left( \log_{10} x \right)^2 + 5 \left( \log_{10} x \right) - 12 = 0 $$ | Propiedad de los reales. |
| 9. | $$ a=\log_{10} x $$ | Sustitución para simplificar el análisis. |
| 10. | $$ 3a^2+5a-12=0 $$ | Sustitución de 9 en 8. |
| 11. | $$ a_{1,2}=\frac{-5 \pm \sqrt{5^2-4(3)(-12)}}{2(3)} $$ | Aplico fórmula para solución de ecuación cuadrática de la forma \(Ax^2+Bx+C=0\). |
| 12. | $$ a_{1,2}=\frac{-5 \pm \sqrt{25+144}}{6} $$ | De 11. |
| 13. | $$ a_1=\frac{4}{3} $$ | De 12. Con la suma en el numerador. |
| 14. | $$ a_2=-3 $$ | De 12. Con la diferencia en el numerador. |
| 15. | $$ a_1=\log_{10} x=\frac{4}{3} $$ | Transitividad entre 9 y 13. |
| 16. | $$ x=10^{\frac{4}{3}} \approx 21.54 $$ | De 15. Por la definición de la función logarítmica. Solución 1. |
| 17. | $$ a_2=\log_{10} x=-3 $$ | Transitividad entre 9 y 14. |
| 18. | $$ x=10^{-3} = 0.001 $$ | De 17. Por la definición de la función logarítmica. Solución 2. |
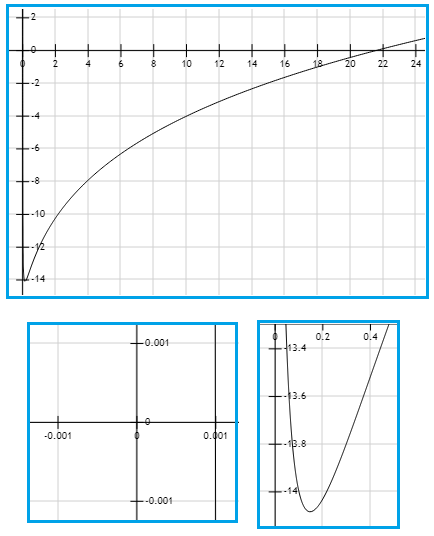
Figura 1. Gráfica de la función \( f(x) = 3 \left( \log_{10} x \right)^2 + 5 \left( \log_{10} x \right) - 12 \). Ver paso 8.




Comentarios potenciados por CComment