El dominio de una función

Visto: 618

Contenido

Al matemático francés P. G. Lejeune Dirichlet (1805-1859) se le otorga el reconocimiento de la definición moderna de función.

Definición de función

Una función es una regla que asigna a cada elemento de un conjunto (llamado el dominio de la función) exactamente un valor de otro conjunto. El conjunto de todos los valores asignados se llama el rango de la función.

Dominio y rango

El dominio es el conjunto de elementos a los que la función asigna valores. Cuando no se especifica ningún dominio, el acuerdo general es que el dominio es el mayor conjunto de números reales en el que sigue siendo válida la regla de correspondencia de la función, y que produce valores en los números reales. A este conjunto se le llama dominio natural de la función.

El dominio de una función polinómica

No importa el grado del polinomio, toda función polinómica de la forma

$$ f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x^1+a_0x^0 $$

tiene como dominio a todo el conjunto de los números reales. Es decir,

$$ D_f= -\infty < x < +\infty $$

$$ \{(-\infty, +\infty)\} $$

El dominio de funciones racionales

El dominio de una función de la forma

$$ f(x)=\frac{p(x)}{q(x)} $$

debe calcularse teniendo en cuenta excluir todos los valores para \(x\) que hacen cero el denominador \(q(x)\). Se debe entonces resolver la ecuación \(q(x)=0\) y excluir la solución del conjunto de los reales. Cuando se evalúa uno de estos valores en \(q(x)\) el valor de \(f(x)\) tiende a ser \(-\infty\) o \(+\infty\). En resumen, el dominio de una función racional es, al menos, todo el conjunto de los reales menos los ceros de \(q(x)\):

$$ D_f=\mathbb{R}-\left(q(x)=0\right) $$

El dominio de funciones irracionales

Las funciones irracionales son aquellas en donde la variable independiente está bajo el signo del radical. En funciones irracionales, se excluyen del dominio los valores para \(x\) que hacen a \(f(x)\) igual a la raíz par de un número negativo. Si la raíz es impar, la función bajo el radical puede tener cualquier valor real (es decir, el dominio es todo el conjunto de los reales). A continuación se presenta una tabla con los casos que pueden presentarse y la forma de calcular el dominio correspondiente.

Forma general Variante

Formas

particulares

 Dominio Ejemplo
$$ \sqrt[k]{A} $$ \(k\) impar $$ \sqrt[k]{p(x)} $$ $$ \mathbb{R} $$

$$ f(x)=\sqrt[3]{x^3+x-1} $$

Dominio: \( \mathbb{R} \)
$$ \sqrt[k]{\frac{p(x)}{q(x)}} $$ $$ \mathbb{R}-\left[q(x)=0\right] $$

$$ f(x)=\sqrt[5]{\frac{2x+1}{x^2-x-2}} $$

Dominio: \(\mathbb{R}-\{-1,2\}\).
\(k\) par $$ \sqrt[k]{p(x)} $$ $$ p(x) \geq 0 $$

$$ f(x)=\sqrt[12]{x^2-x-2} $$

Dominio:

$$ (-\infty,-1] \cup [2,+\infty) $$
$$ \sqrt[k]{\frac{p(x)}{q(x)}} $$

$$ \frac{p(x)}{q(x)} \geq 0 $$

y

$$ q(x) \neq 0 $$

$$ f(x)=\sqrt[8]{\frac{2x+11}{x^2-x-2}} $$

Dominio:

$$ \left[\frac{-11}{2},-1\right) \cup (2,+\infty) $$

Ejemplo para función polinómica

Hallar el dominio de la función

$$ g(x)=x^3-1 $$

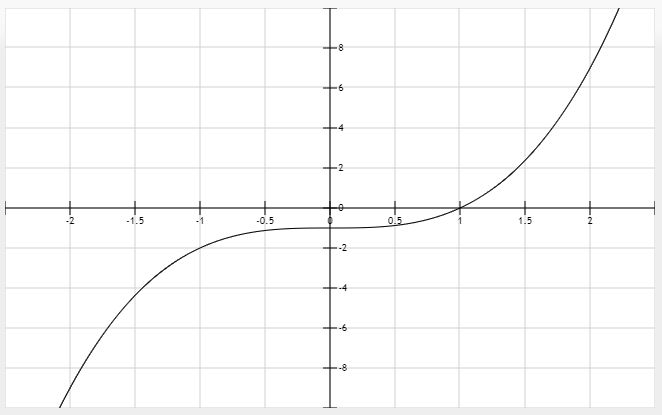
El dominio es el conjunto de todos los números reales. La variable \(x\) puede tomar cualquier valor entre los números reales. Se puede escribir que el conjunto solución es:

$$ \boxed{D_f= -\infty < x < \infty} $$

Alternativamente,

$$ \boxed{(-\infty, \infty)} $$

Ejemplo 1 para función racional (división por cero)

Hallar el dominio de la función

$$ h(x)=\frac{1}{x-1} $$

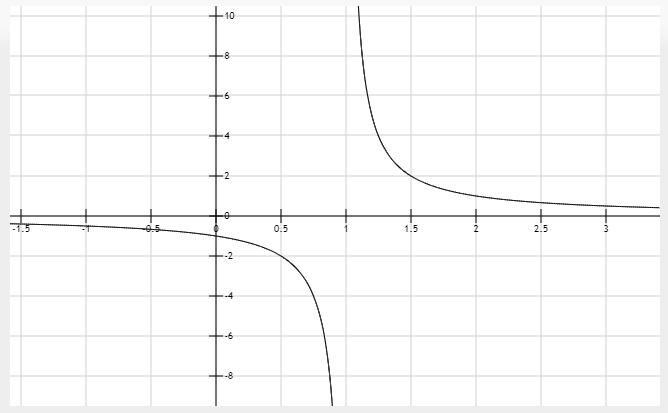
El dominio natural consiste de todos los números reales excepto el 1. Se excluye al número 1 para evitar la división entre cero. En este caso, se resolvió la ecuación \(x-1=0\) para encontrar el dominio de la función. El dominio es:

$$ \boxed{D_f= \mathbb{R}-\{1\}} $$

Ejemplo 2 para función racional (división por cero)

Hallar el dominio de

$$ f(x)=\frac{2x-3}{x+7} $$

El numerador de la función puede tomar cualquier valor de \(x\) real, pero cuando \(x=-7\) el valor de \(f(x)\) resulta

$$ f(-7)=\frac{(2)(-7)-3}{(-7)+7}=\frac{-17}{0} \rightarrow f(-7)=\pm \infty $$

Cuando el valor de \(x\) se acerca a \(x=-7\) con valores menores que -7 o mayores que -7 el valor de \(f(-7)\) tiende a \(\pm \infty\). Haz la prueba:

\(x\) \(f(x)\)
-6 -15
-6.5 -32
-6.75 -66
-6.875 -134
-7 \(\pm \infty\)
-7.125 138
-7.25 70
-7.5 36
-8 19

La gráfica de la función es

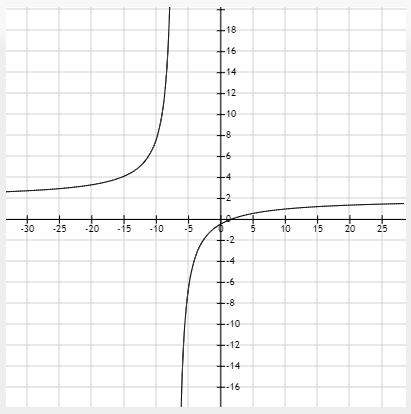
En conclusión, el dominio de la función es

$$ \boxed{D_f= \mathbb{R}-\{-7\}} $$

$$ \boxed{{(-\infty,-7) \cup (-7,+\infty)}} $$

Ejemplo 3 para función racional (división por cero)

Hallar el dominio natural de

$$ f(x)=\frac{4x}{(x+2)(x-3)} $$

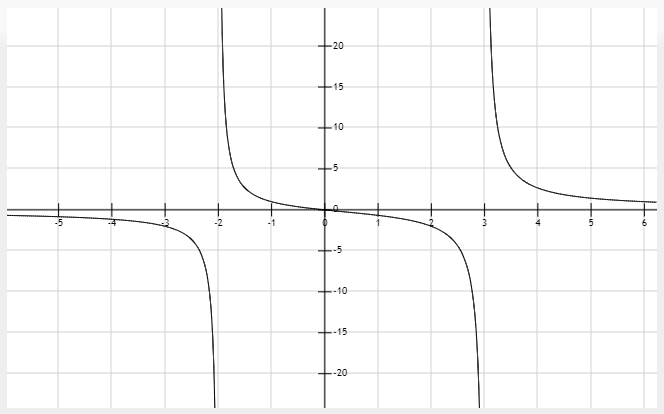
La variable \(x\) en el numerador puede tomar cualquier valor real, pero el producto en el denominador sólo puede tomar valores tal que

$$ (x+2)(x-3) \neq 0 $$

Para hallarlos se resuelve la ecuación

$$ (x+2)(x-3) = 0 $$

Esto resulta en

$$ x+2=0 $$

$$ x=-2 $$

Del mismo modo

$$ x-3=0 $$

$$ x=3 $$

El dominio consiste de todos los números reales excepto -2 y 3.

$$ \boxed{D_f=\mathbb{R}-\{-2,3\}} $$

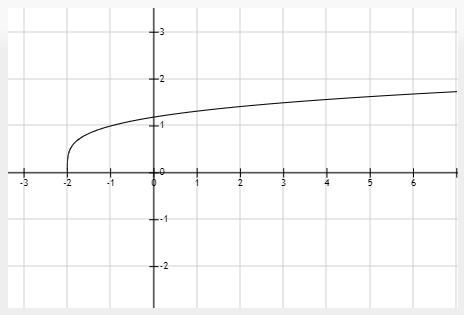
Ejemplo para función irracional (raíz par de número negativo)

Hallar el dominio de la función

$$ f(x)=\sqrt[4]{x+2} $$

Recordar que las raíces pares de números negativos no pertenecen al conjunto de los números reales. Por ese motivo, se debe resolver la inecuación

$$ x+2 \geq 0 $$

$$ x \geq -2 $$

El dominio de la función será, entonces

$$ \boxed{D_f= x \geq -2} $$

$$ \boxed{[-2, +\infty)} $$

La gráfica de la función es

Otros ejemplos

Indicar el dominio y rango de las siguientes reglas (funciones).

REGLA DOMINIO RANGO
\(F(x)=4x\) Todos los reales Todos los reales
\(G(x)=\sqrt{x-3}\) \({D_f=x \geq 3}\) Reales no negativos
\(H(x)=\frac{1}{(x-2)^2}\) \({D_f=x \neq 2}\) Reales positivos

Resumen: ¿Cuándo un valor de \(x\) no puede estar incluido en el dominio?

No estará en el dominio cuando al evaluar \(x\) el valor de \(f(x)\) sea:

  1. Caso 1: \(f(x)=-\infty\) o \(f(x)=+\infty\). Es decir, existe división por cero.
  2. Caso 2: \(f(x)\) sea igual a la raíz par de un número negativo. Si la raíz es impar, la función bajo el radical puede tener cualquier valor real (es decir, el dominio es todo el conjunto de los reales).

Comentarios potenciados por CComment