2. (Dificultad: 8/10) Resolver para \(x\) la siguiente ecuación:
$$ (\sqrt{x})^x = x^\sqrt{x} $$
Solución
La solución de la ecuación del tipo exponencial es:
| 1. | $$ (\sqrt{x})^x = x^\sqrt{x} $$ | |
| 2. | $$ x^{\frac{x}{2}} = x^\sqrt{x} $$ | Operamos con la raíz del lado izq. |
| 3. | $$ \ln{\left( x^{\frac{x}{2}} \right)} = \ln{\left( x^\sqrt{x} \right)} $$ | Log. natural a ambos lados. |
| 4. | $$ \frac{x}{2} \ln{x} = \sqrt{x} \ln{x} $$ | Por ley de logaritmos. |
| 5. | $$ \frac{x}{2} \ln{x} - \sqrt{x} \ln{x} = 0$$ | Prop. de reales. |
| 6. | $$ \ln{x} \left( \frac{x}{2} - \sqrt{x} \right) = 0$$ | Factor común Ln(x) |
| 7. | $$ \ln{x}=0 $$ | Primera posibilidad. |
| 8. | $$ \frac{x}{2} - \sqrt{x}=0 $$ | Segunda posibilidad. |
| 9a. | $$ e^{\ln{x}}=e^0 $$ | De 7. Función exponencial. |
| 10a. | $$ x=1 $$ | Solución para \(\ln{x}=0\) |
| 11b. | $$ \frac{x^2}{4}=x $$ | De 8. Paso raiz al otro lado y elevo al cuadrado ambos lados. |
| 12b. | $$ x^2=4x $$ | Prop. de reales. |
| 13b. | $$ x^2-4x=0 $$ | Prop. de reales. |
| 14b. | $$ x(x-4)=0 $$ | Factor común x. |
| 15b. | $$ x=0~~~ó~~~x=4 $$ | Dos posibilidades de solucion para \( \frac{x}{2} - \sqrt{x}=0 \) |
Si evaluamos \(x=0\) se puede observar que se produce una indeterminación del tipo \(0^0\), luego \(x=0\) no pertenece al dominio de las funciones y no existiría solución en \(x=0\). Por lo tanto, las dos soluciones son:
$$ x=1~~~y~~~x=4 $$
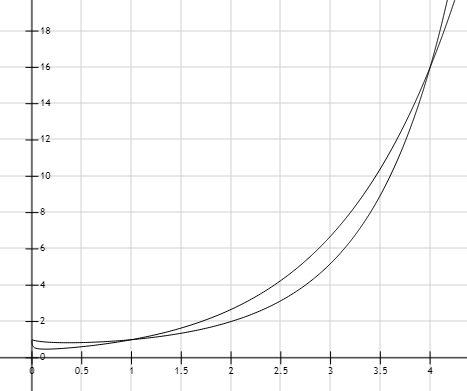
Curvas de las funciones \( \left( \sqrt{x} \right)^x\) y \(x^{\sqrt{x}}\)




Comentarios potenciados por CComment