3. (Dificultad: 5/10) Resolver la siguiente ecuación exponencial para x:
$$ 2 \left( 3^{2x-4} \right) - 7 \left( 3^{x-2} \right) + 6 =0 $$
Solución
La solución es la siguiente:
| Proposición | Razón | |
| 1. | $$ 2 \left( 3^{2x-4} \right) - 7 \left( 3^{x-2} \right) + 6 =0 $$ | |
| 2. | $$ 2 \left( 3^{2(x-2)} \right) - 7 \left( 3^{x-2} \right) + 6 =0 $$ | Factor común 2. |
| 3. | $$ 2 \left( 3^{x-2} \right)^2 - 7 \left( 3^{x-2} \right) + 6 =0 $$ | Aplico propiedades de exponentes. |
| 4. | Si \( a=3^{x-2} \): | |
| 5. | $$ 2a^2-7a+6=0 $$ |
Sustitución de 4 en 3. Forma cuadrática: $$ Ax^2+Bx+C=0 $$ |
| 6. | $$ a_{1,2}=\frac{-(-7) \pm \sqrt{(-7)^2-4(2)(6)}}{2(2)} $$ | De 5. Solución de ecuación cuadrática. |
| 7. | $$ a_{1,2}=\frac{7 \pm \sqrt{49-48}}{4} $$ | De 6. |
| 8. | $$ a_{1,2}=\frac{7 \pm 1}{4} $$ | De 7. |
| 9. | $$ a_1=\frac{7 + 1}{4} = 2 $$ | De 8. Solución 1. |
| 10. | $$ a_2=\frac{7 - 1}{4} = \frac{3}{2} $$ | De 8. Solución 2. |
| 11a. | $$ a_1=3^{x-2}=2 $$ | Por transitividad entre 4 y 9. |
| 12a. | $$ \ln{ \left( 3^{x-2} \right) } = \ln{(2)} $$ | De 11a. Calculo logaritmo natural a ambos lados. |
| 13a. | $$ (x-2) \ln{(3)} = \ln{(2)} $$ | De 12a. Por ley de logaritmos. |
| 14a. | $$ x - 2 = \frac{\ln{(2)}}{\ln{(3)}} $$ | De 13a. Propiedad de los reales. |
| 15a. |
$$ x =2 + \frac{\ln{(2)}}{\ln{(3)}} $$ \(x=\) 2.631 |
De 14a. Propiedad de los reales. Solución 1. |
| 16b. | $$ a_2=3^{x-2}=\frac{3}{2} $$ | Por transitividad entre 4 y 10. |
| 17b. | $$ \ln{ \left( 3^{x-2} \right) } = \ln{\frac{3}{2}} $$ | De 16b. Calculo logaritmo natural a ambos lados. |
| 18b. | $$ (x-2) \ln{(3)} = \ln{(3)} - \ln{(2)} $$ | De 17b. Por leyes de logaritmos. |
| 19b. | $$ x - 2 = \frac{\ln{(3)} - \ln{(2)}}{\ln{(3)}} $$ | De 18b. Propiedad de los reales. |
| 20b. | $$ x = 2 + 1 - \frac{\ln{(2)}}{\ln{(3)}} $$ | De 19b. Propiedad de los reales. |
| 21b. |
$$ x = 3 - \frac{\ln{(2)}}{\ln{(3)}} $$ \(x=\) 2.369 |
De 20b. Propiedad de los reales. Solución 2. |
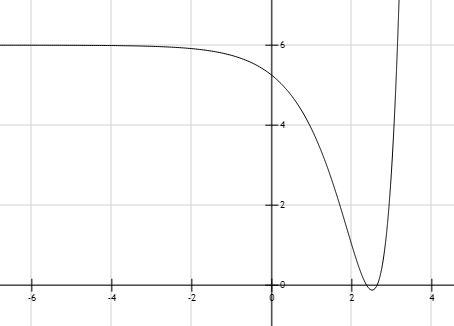
Figura 1. Curva de la función \( 2 \left( 3^{2x-4} \right) - 7 \left( 3^{x-2} \right) + 6 =0 \)
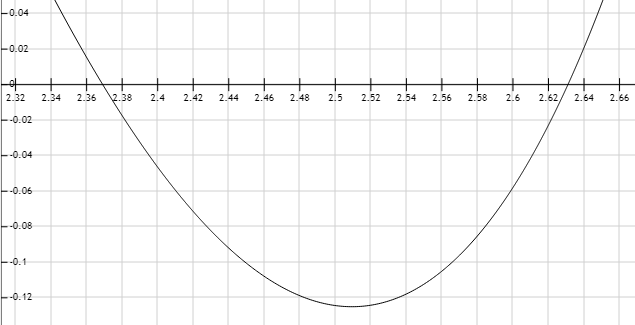
Figura 2. Curva de la función \( 2 \left( 3^{2x-4} \right) - 7 \left( 3^{x-2} \right) + 6 =0 \)
Acercamiento a las soluciones: la coordenada \(x\) de los interceptos de la curva con la recta \(y=0\)




Comentarios potenciados por CComment