5. (Dificultad: 5/10) Resolver para \(x\) la siguiente ecuación:
$$ 4^{x-1}+23 = 9 \left(2^{x-1}+1\right) $$
Solución
Proposición |
Razón |
|
| 1. | $$ 4^{x-1}+23 = 9 \left(2^{x-1}+1\right) $$ | Planteamiento del problema. |
| 2. | $$ \left(2^2\right)^{x-1}+23-9\left(2^{x-1}\right) - 9 = 0 $$ | De 1. |
| 3. | $$ \left(2^{x-1}\right)^2 - 9\left(2^{x-1}\right) +14 = 0 $$ | De 2. Propiedades de los exponentes. |
| 4. | $$ \text{Si}~a=2^{x-1} $$ | Definición de nueva variable. |
| 5. | $$ a^2-9a+14=0 $$ | Sustitución de 4 en 3. Ecuación cuadrática. |
| 6. | $$ \left(a-2\right)\left(a-7\right)=0 $$ | De 5. Se factoriza el polinomio. |
| 7. | $$ \text{Para}~a-2=0 $$ | De 6. Solución 1. |
| 8. | $$ a=2=2^{x-1} $$ | De 7 y 4. |
| 9. | $$ x-1=1 $$ | De 8. Se igualan exponentes dado que se posee la misma base. |
| 10. | $$ x=2 $$ | De 9. Propiedad de los reales. |
| 11. | $$ \text{Para}~a-7=0 $$ | De 6. Solución 2. |
| 12. | $$ a=7=2^{x-1} $$ | De 11 y 4. |
| 13. | $$ \log_2 7=\log_2 2^{x-1}$$ | Se toma logaritmo base 2 a ambos lados. |
| 14. | $$ \log_2 7= x-1$$ | De 13. El logaritmo base 2 de 2 es igual a 1. Por ley de logaritmos el exponente pasa a multiplicar. |
| 15. | $$ x=1+\log_2 7$$ | De 14. Propiedades de los reales. |
| 16. | $$ x=1+\frac{\ln7}{\ln2}=3.81$$ | De 15. Cambio de base. |
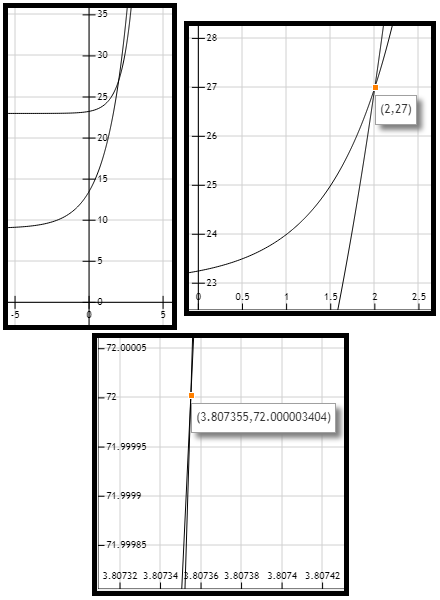
Figura 1. Gráficas de las curvas de las funciones \( f(x)=4^{x-1}+23 \) y \(f(x)=9 \left(2^{x-1}+1\right) \).




Comentarios potenciados por CComment