6. (Dificultad: 5 /10) Resolver para \(x\) la siguiente ecuación:
$$ e^x + e^{-x} =2$$
Solución
Proposición |
Razón |
|
| 1. | $$ e^x + e^{-x} =2$$ | Planteamiento del problema. |
| 2. | $$ e^x + \frac{1}{e^x} = 2$$ | De 1. Propiedad de los exponentes. |
| 3. | $$ \frac{e^x \cdot e^x}{e^x} + \frac{1}{e^x}=2$$ | De 2. Propiedad de los reales. |
| 4. | $$ \frac{e^{2x} + 1}{e^x}=2$$ | De 3. Suma de fracciones. |
| 5. | $$ e^{2x} + 1=2e^x$$ | De 4. Propiedad de los reales. |
| 6. | $$ \left(e^x\right)^2 - 2e^x + 1=0 $$ | De 5. Propiedad de los reales. |
| 7. | $$ \left(e^x-1\right)^2 =0 $$ | De 6. Se factoriza el polinomio cuadrático. |
| 8. | $$ e^x = 1 $$ | De 7. Propiedad de los reales. Cero de multiplicidad 2. |
| 9. | $$ \ln{e^x} = \ln{1} $$ | Se toma logaritmo natural a ambos lados. |
| 10. | $$ x \ln{e} = \ln{1} $$ | De 9. Ley de logaritmos. |
| 11. | $$ \ln{e}=1~~~\text{y}~~~\ln{1}=0 $$ | Por la definición del logaritmo natural. |
| 12. | $$ x=0 $$ | De 11 en 10. Solución. |
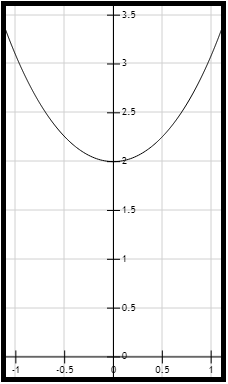
Figura 1. Gráfica de la curva \( f(x) = e^x + e^{-x} \).




Comentarios potenciados por CComment