7. (Dificultad: 6/10) Resolver para \(x\) la siguiente ecuación:
$$ 3^x+3^{x-1}+3^{x-2}+3^{x-3}+3^{x-4}=363 $$
Solución
Proposición |
Razón |
|
| 1. | $$ 3^x+3^{x-1}+3^{x-2}+3^{x-3}+3^{x-4}=363 $$ | Planteamiento del problema. |
| 2. | $$ 3^x+3^x 3^{-1}+3^x 3^{-2}+3^x 3^{-3}+3^x 3^{-4}=363 $$ | De 1. Por propiedad de los exponentes. |
| 3. | $$ 3^x \left( 1+3^{-1}+3^{-2}+3^{-3}+3^{-4} \right) = 363 $$ | De 2. Se factoriza al lado izquierdo. |
| 4. | $$ 3^x \left( 1+\frac{1}{3^{1}}+\frac{1}{3^{2}}+\frac{1}{3^{3}}+\frac{1}{3^{4}} \right) = 363 $$ | De 3. Por propiedad de los exponentes. |
| 5. | $$ 3^x \left( \frac{3^4}{3^4}+\frac{3^3}{3^{4}}+\frac{3^2}{3^{4}}+\frac{3^1}{3^{4}}+\frac{1}{3^{4}} \right) = 363 $$ | De 4. Por propiedad de los reales. |
| 6. | $$ 3^x \left( \frac{3^4+3^3+3^2+3^1+1}{3^4} \right) = 363 $$ | De 5. Suma de fracciones. |
| 7. | $$ 3^x \left( \frac{81+27+9+3+1}{3^4} \right) = 363 $$ | De 6. |
| 8. | $$ 3^x \left( \frac{121}{3^4} \right) = 121 \times 3 $$ | De 7. |
| 9. | $$ 3^x = \frac{121 \times 3^5}{121} $$ | De 8. |
| 10. | $$ 3^x = 3^5 $$ | De 9. |
| 11. | $$ \log_3 3^x=\log_3 3^5 $$ | De 10. Calculo logaritmo base 3 a ambos lados. |
| 12. | $$ x \log_3 3=5 \log_3 3 $$ | De 11. Por ley de logaritmos. |
| 13. | $$ \log_3 3^1 = y~~~\text{si}~~~3^1 = 3^y~\rightarrow y=1 $$ | Recordar la definición del logaritmo de un número. |
| 14. | $$ x = 5 $$ | De 13 en 12. Solución. |
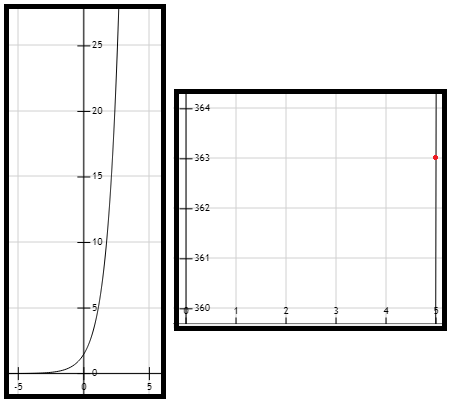
Figura 1. Gráfica de la curva \( f(x) = 3^x+3^{x-1}+3^{x-2}+3^{x-3}+3^{x-4}=363 \).




Comentarios potenciados por CComment