1. (Dificultad: 7/10) Factorizar y hallar las raices (los ceros) reales del siguiente polinomio:

$$ f(x)=x^5-5x^4+12x^3-24x^2+32x-16 $$

Solución

El teorema del número de ceros reales de un polinomio menciona que no puede tener más ceros reales que su grado. Dado que el polinomio de este problema es de grado 5, se sabe entonces que tiene a lo sumo 5 ceros reales. Para determinar los posibles ceros racionales de \(f(x)\) se debe usar el teorema de los ceros racionales en conjunto con la regla de los signos de Descartes para hallar los posibles ceros del polinomio. Un primer grupo posible de raíces se halla como sigue a continuación:

---

Teorema de los ceros racionales

Sea \(f(x)\) una función polinomial de grado 1 o mayor de la forma:

$$ f(x)=a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x^1 + a_0 $$

con \(a_n \neq 0\) y \(a_0 \neq 0\), donde cada coeficiente es un entero. Si \(p/q\) es un cero racional de \(f(x)\), entonces \(p\) debe ser un factor de \(a_0\) y \(q\) debe ser un factor de \(a_n\).

---

Una primera lista de ceros racionales posibles de \(f(x)\) se halla obteniendo los factores de \(a_0\) y \(a_n\), así:

Factores de \(a_0\):

	$$ 1 \times -16 $$
	$$ -1 \times 16 $$
$$ a_0=-16=~~~$$	$$ 2 \times -8 $$
	$$ -2 \times 8 $$
	$$ 4 \times -4 $$

Los factores de \(a_0\) son:

$$ p:\pm 1,\pm 2,\pm 4,\pm 8,\pm 16 $$

Factores de \(a_5\):

$$ a_5=1=~~~$$	$$ 1 \times 1 $$
	$$ -1 \times -1 $$

Los factores de \(a_5\) son:

$$ q:~\pm 1 $$

Ahora se forman todas las razones posibles \(p/q\), resultando:

$$ \frac{p}{q}:~\pm 1,~\pm 2,~\pm 4,~\pm 8,~\pm 16~~~\text{[1]}$$

Este es un primer grupo posible de raíces racionales del polinomio, sin embargo, se debe aplicar la regla de los signos de Descartes para acotar aún más este grupo.

---

Regla de los signos de Descartes

Se emplea para hallar el número y localización de los ceros (las raíces) reales. Requiere hallar el número de variaciones en el signo de los coeficientes de \(f(x)\) y \(f(-x)\).

a. Para \(f(x)\): el número de ceros reales positivos es igual al número de variaciones de signo o a ese número menos un entero par.

b. Para \(f(-x)\): el número de ceros reales negativos es igual al número de variaciones de signo o a ese número menos un entero par.

Es decir, esta regla permite hallar el número total de ceros reales, que resultan de sumar el número de ceros reales positivos y negativos.

---

Continuando con la solución de nuestro problema, lo primero que debemos hacer es llevar el polinomio a la forma estándar, es decir, escribir los términos con las potencias de \(x\) en orden descendente. El polinomio de nuestro problema ya se encuentra ordenado de esta manera, luego, podemos escribir igual:

a. Para \(f(x)\):

$$ f(x)=x^5-5x^4+12x^3-24x^2+32x-16 $$

El número de variaciones de signo, en orden, de izquierda a derecha, es: + a - (una), - a + (dos), + a - (tres), - a + (cuatro), + a - (cinco). Entonces, como dice la regla de los signos de Descartes, existen cinco, tres o ningún cero real positivo.

b. Para \(f(-x)\):

$$ f(-x)=-x^5-5x^4-12x^3-24x^2-32x-16 $$

El número de variaciones de signo es cero, dado que el signo de los coeficientes permanece negativo para todos los términos, por lo cual, no se tienen ceros reales negativos para este polinomio.

En conclusión, como el polinomio no tiene ceros reales negativos, el conjunto de ceros racionales posibles de \([1]\) se reduce a:

$$ \frac{p}{q}:~1,~2,~4,~8,~16~~~\text{[2]}$$

Una vez se tiene el conjunto de ceros racionales posibles se puede usar división sintética o el teorema del factor para comprobar cual de los ceros racionales posibles de \([2]\) es útil para empezar el proceso de factorización. Usemos el teorema del factor.

---

Teorema del factor

Sea \(f\) una función polinomial, entonces \( (x-c) \) es un factor de \( f(x) \) si y sólo si \( f(c)=0 \). De aquí se desprenden dos proposiciones:

a. Si \( f(c)=0 \) entonces \( (x-c) \) es un factor de \( f(x) \).

b. Si \( (x-c) \) es un factor de \( f(x) \) entonces \( f(c)=0 \).

---

Tomemos uno por uno los números en \([2]\) y comprobemos si alguno es un cero. Para \( x=1 \):

$$ f(1)=(1)^5-5(1)^4+12(1)^3-24(1)^2+32(1)-16 $$

$$ f(1)=1-5+12-24+32-16 $$

$$ f(1)=0 $$

El resultado anterior indica que el número 1 es una raíz o un cero del Polinomio. Además, por el Teorema del factor, podemos decir que si \( f(1)=0 \) entonces \( (x-1) \) es un factor del polinomio \( f(x) \). Otra manera de comprobar que el número 1 es una raíz o un cero (es lo mismo) es realizar la división sintética del polinomio sobre \( (x-1) \) y comprobar que el residuo es cero. Para continuar con la factorización, usemos la división sintética para hallar el cociente que multiplicado por \( (x-1) \) resulte en el polinomio original:

---

División sintética

Los números en negrilla (primera fila, fondo blanco) son los coeficientes del polinomio, en orden. Primero, tomo el primer coeficiente en la primera fila (1), lo copio en la última fila y lo multiplico por \(c=1\). El resultado lo ubico debajo del segundo coeficiente (-5). Sumo -5+1=-4 y luego multiplico -4 nuevamente por \(c=1\). Escribo el resultado -4 debajo del tercer coeficiente (12) y sumo 12-4=8, y así sucesivamente hasta obtener el residuo 0 (en la esquina de la tabla, ultima fila hacia abajo y última columna hacia la derecha). Este era el resultado esperado, dado que ya habíamos comprobado que \(c=1\) es un cero del polinomio.

$$ c=1 $$	1	-5	12	-24	32	-16
		1	-4	8	-16	16
	1	-4	8	-16	16	0

El polinomio que es el cociente es un grado menor que el dividendo \( f(x) \):

$$ g(x)=x^4-4x^3+8x^2-16x+16 $$ 

Se requiere tomar el primer factor \( (x-1) \) que ya habíamos hallado aplicando el teorema del factor y el cociente hallado. El resultado parcial del proceso de factorización es, entonces:

$$ f(x)=(x-1)(x^4-4x^3+8x^2-16x+16) $$

Recordar que se debe cumplir que:

$$ (\text{Cociente})(\text{Divisor})+\text{Residuo}=\text{Dividendo} $$

Se continúa el proceso de factorización del polinomio \( f(x) \) factorizando ahora \( g(x) \). Los ceros posibles siguen siendo los mismos, luego, de \([2]\).

$$ \frac{p}{q}:~1,~2,~4,~8,~16$$

Se usa el teorema del factor para comprobar si 1 es un cero de \(g(x)\):

$$ g(1)=(1)^4-4(1)^3+8(1)^2-16(1)+16 $$ 

$$ g(1)=1-4+8-16+16 $$ 

$$ g(1)=5 $$

Luego, 1 no es un cero de \( g(x) \). Se prueba con 2:

$$ g(2)=(2)^4-4(2)^3+8(2)^2-16(2)+16 $$ 

$$ g(2)=16-32+32-32+16 $$ 

$$ g(2)=0 $$ 

Luego, 2 es un cero de \( g(x) \) y, por el teorema del factor, \( (x-2) \) es un factor de \( g(x) \). Se realiza la división sintética para hallar el cociente:

$$ c=2 $$	1	-4	8	-16	16
		2	-4	8	-16
	1	-2	4	-8	0

Al usar el último renglón se encuentra, con un grado menor:

$$ h(x)=x^3-2x^2+4x-8 $$

La factorización obtenida hasta ahora es:

$$ f(x)=(x-1)(x-2)(x^3-2x^2+4x-8) $$

Se podría factorizar \( h(x) \) agrupando términos:

$$ h(x)=(x^3-2x^2)+(4x-8) $$

$$ h(x)=x^2(x-2)+4(x-2) $$

$$ h(x)=(x-2)(x^2+4) $$

También es posible utilizar por última vez la división sintética para hallar un cociente para \( h(x) \). Los ceros posibles siguen siendo los contenidos en \([2]\) a excepción del número 16:

$$ \frac{p}{q}:~1,~2,~4,~8$$

Es posible verificar que \(h(1)=-5\), luego, no es un cero. Cuando se prueba el número 2, se encuentra \( h(2)=0 \), por lo tanto, \( x=2 \) es un cero de \(h(x)\) y \( (x-2) \) es un factor de \( h(x) \). Realizamos la división sintética para hallar el cociente de \( h(x) \):

$$ c=2 $$	1	-2	4	-8
		2	0	8
	1	0	4	0

El residuo es cero, como se esperaba. Al usar el último renglón se encuentra, con un grado menor:

$$ m(x)=x^2+0x+4 $$

$$ m(x)=x^2+4 $$

Se obtiene entonces para este último polinomio:

$$ h(x)=(x-2)(x^2+4) $$

Finalmente, el proceso de factorización completo obtenido resulta:

$$ f(x)=(x-1)(x-2)(x-2)(x^2+4) $$

$$ f(x)=(x-1)(x-2)^2(x^2+4) $$

Los ceros del polinomio se han venido obteniendo en el transcurso del ejercicio, sin embargo, se pueden volver a obtener escribiendo:

$$ (x-1)(x-2)^2(x^2+4)=0 $$

Luego,

Si \( x-1=0 \) se obtiene \( x=1 \).

Si \( x-2=0 \) se obtiene \( x=2 \).

Si \( x^2+4=0 \) resulta que al resolver esta ecuación cuadrática, no se obtienen soluciones reales.

Los ceros reales de \(f(x)\) son 1 y 2, siendo 2 un cero de multiplicidad 2. La forma factorizada de \( f(x) \) es, finalmente:

$$ f(x)=x^5-5x^4+12x^3-24x^2+32x-16=(x-1)(x-2)^2(x^2+4) $$

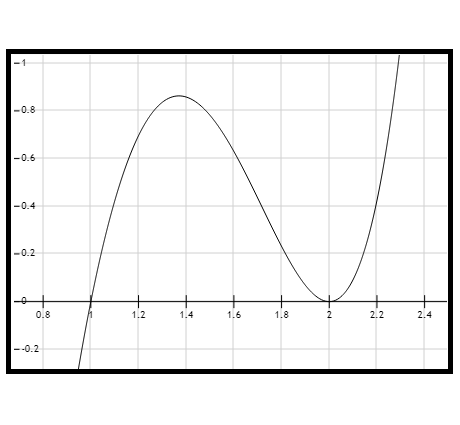
Figura 1. Gráfica de la curva de la función \( f(x)=x^5-5x^4+12x^3-24x^2+32x-16=(x-1)(x-2)^2(x^2+4) \).