4. (Dificultad: 7/10) Exprese al siguiente polinomio como un producto de factores lineales. Escriba al final las raices o ceros del polinomio.
$$ f(x) = x^4+x^3-5x^2-15x-18 $$
Solución
Primero se hallan los factores de \(a_0=-18\):
$$ -18=2 \times -9,~-2 \times 9,~3 \times -6,~-3 \times 6,~1 \times -18,~-1 \times 18 $$
Luego, los factores son: \(p=\pm 1,~\pm 2,~\pm 3,~\pm 6,~\pm 9,~\pm 18 \). A continuación, se hallan los factores de \(a_n=1\):
$$ 1=1 \times 1,~-1 \times -1 $$
Entonces, los factores son: \(q=\pm 1\).
Los posibles ceros racionales son las combinaciones \(p/q\) de los números anteriores. Se puede evaluar cada \(p/q\). Primero el número +1, luego el -1 y así sucesivamente. Por suerte \(p/q=-2\) es un cero:
$$ f(-2)=0 $$
Por ese motivo \((x-(-2)) = (x+2)\) es un factor del polinomio \(f(x)\). Conociendo entonces un factor, se puede aplicar división sintética para hallar el otro factor:
| c=-2 | 1 | 1 | -5 | -15 | -18 |
| -2 | 2 | 6 | 18 | ||
| 1 | -1 | -3 | -9 | 0 (el residuo) |
Se toman los números de la última fila como los coeficientes del polinomio resultante, el cual es un grado menor que el polinomio original. La factorización se halla en el siguiente estado:
$$ f(x) = x^4+x^3-5x^2-15x-18 = \left( x+2 \right) \left( x^3-x^2-3x-9 \right) = \left( x+2 \right) \cdot g(x)~~~\text{Ec.1} $$
Se busca ahora factorizar el polinomio \(g(x)\) de grado 3 que quedó a la derecha en la expresión anterior. Los factores de \(a_0=-9\) son \(p=\pm 1,~\pm 3,~\pm 9 \). Los factores de \(a_n=1\) son \(q=\pm 1\). Los ceros racionales son las combinaciones posibles \(p/q\). Se puede evaluar uno por uno desde +1, luego -1, luego +3, luego -3, etc. Se hallará que \(g(3)=0\), por lo cual \((x-3)\) es un factor de \(g(x)\). Se usa la división sintética para hallar el otro factor de \(g(x)\).
| c=3 | 1 | -1 | -3 | -9 |
| 3 | 6 | 9 | ||
| 1 | 2 | 3 | 0 (el residuo) |
Se toman los números de la última fila como los coeficientes del polinomio resultante, el cual es un grado menor que el polinomio original. La factorización de \(g(x)\) se puede escribir así:
$$ g(x) = x^3-x^2-3x-9 = (x-3) \left( x^2+2x+3 \right) = (x-3) \cdot h(x)~~~\text{Ec.2} $$
El polinomio \(h(x)\) no posee ceros reales. Esto se puede concluir a partir del análisis de la función o la gráfica de la parábola, la cual es cóncava hacia arriba y mayor que cero para cualquier valor de x. Finalmente, se puede escribir el polinomio original \(f(x)\) teniendo en cuenta los resultados de la Ec.1 y la Ec.2, así:
$$ f(x) = x^4+x^3-5x^2-15x-18 = (x+2)(x-3)(x^2+2x+3) $$
Las raíces (también llamadas "los ceros") del polinomio son:
$$ x=-2 $$
$$ x = 3 $$
En la Figura 1 se presenta el gráfico de \(f(x)\), en donde se pueden apreciar los interceptos de la curva con la recta \(y=0\) o, que es lo mismo, con el eje X:
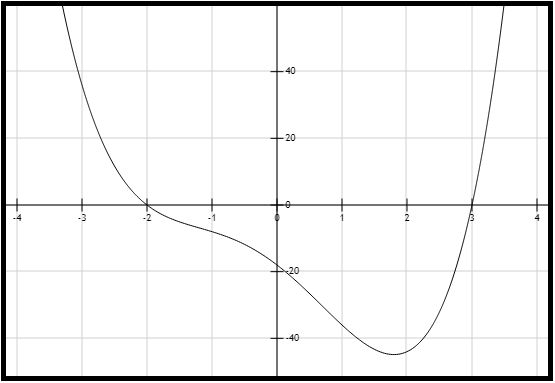
Figura 1. Gráfica de la función \(f(x) = x^4+x^3-5x^2-15x-18\).




Comentarios potenciados por CComment