5. (Dificultad: 4/10) Factorizar el siguiente polinomio y hallar sus raíces racionales.

$$ f(x)=3x^2+x-2 $$

Solución

Debido a que la gráfica de la curva de \(f(x)\) es una parábola, es conveniente tener presente que ésta puede abrir hacia arriba o hacia abajo. En cualquiera de los dos casos, es necesario determinar si la ecuación cuadrática \(f(x)=0\) tiene raíces reales. Esto es fácil de determinar, calculando el valor del discriminante y sometiéndolo a los siguientes dos criterios:

• Si \(b^2-4ac \geq 0\) entonces la ecuación cuadrática tiene dos raíces reales y es posible factorizarla en este campo numérico.
• Si \(b^2-4ac < 0\) entonces la ecuación cuadrática NO tiene raíces reales y, por lo tanto, no es posible factorizarla en este campo numérico.

Siendo así:

$$ b^2-4ac = 1^2-4(3)(-2) = 1 - (-24) = 1+24=25 > 0$$

Debido a esto, el polinomio tiene raíces reales. Ahora, se procede a factorizar. Se elige no usar la fórmula cuadrática esta vez, sino otra aproximación diferente. Dado que los coeficientes a, b y c no tienen factores comunes y \(A \neq 1 \), debemos hallar mediante tanteo dos números \(m\) y \(n\) tal que:

$$ m+n=B=1 $$

$$ m \cdot n = A \cdot B = -6 $$

Estos números son \(m=-2\) y \(n=3\). Ahora, se escribe el polinomio de la siguiente manera:

$$ f(x) = ax^2+bx+c = ax^2+mx+nx+c $$

Es decir:

$$ f(x) = 3x^2+x-2 = 3x^2-2x+3x-2 $$

A continuación, se factoriza por agrupación:

$$ f(x) = 3x^2+x-2 = x \left( 3x-2 \right) + \left( 3x-2 \right) $$

Factorizando los términos comunes:

$$ f(x) = 3x^2+x-2 = \left( x+1 \right) \left( 3x-2 \right) $$

Se puede, inclusive, factorizar el número tres en el paréntesis de la derecha. Al resolver la ecuación \(f(x)=0\) estamos hallando las coordenadas \(x\) donde la curva intercepta la recta \(y=0\) o, dicho de otra manera, hallando las coordenadas donde la curva de \(f(x)\) intercepta al eje X. Se obtiene entonces:

$$ f(x) = 3x^2+x-2 = 3 \left( x+1 \right) \left( x-\frac{2}{3} \right) =0 $$

Los ceros o raíces del polinomio de segundo grado son, finalmente:

$$ \text{Para}~x+1=0 \rightarrow x=-1 $$

$$ \text{Para}~x-\frac{2}{3}=0 \rightarrow x=\frac{2}{3} = 0.667 $$

La gráfica de la función \(f(x)\) se presenta en la Figura 1:

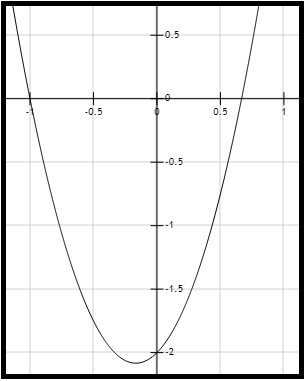
Figura 1. Gráfica de la función \(f(x)=f(x)=3x^2+x-2 \).