6. (Dificultad: 2/10) Factorizar el siguiente polinomio de segundo grado:

$$f(x) = x^2+2x+3$$

Solución

Lo primero que siempre se debe comprobar es la existencia de soluciones para la ecuación:

$$f(x) = x^2+2x+3 = 0$$

Se usa el discriminante para saberlo:

$$b^2-4ac = 2^2-4(1)(3) = 4 - 12 = -8 < 0$$

Si el discriminante es mayor o igual que cero el polinomio posee al menos una raíz, pero si es menor que cero la ecuación cuadrática no tiene raíces reales y por lo tanto no es posible factorizarla sobre este campo numérico. Este último es nuestro caso en este ejercicio. Conclusión: el polinomio es irreducible en los reales.

La razón: la parábola está desplazada en Y, quedando toda por encima o toda por debajo del eje X. Dicho en otras palabras, la ecuación $f(x)=y=0$ no tiene solución. Observe la Figura 1, que ilustra este hallazgo.

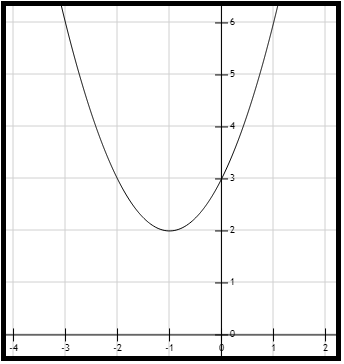
Figura 1. Gráfica de la función $f(x) = x^2+2x+3$.