8. (Dificultad: 5/10) Factorice el siguiente polinomio:

$$ f(x) = 4x^2-x-7 $$

Solución

Lo primero es cerciorarse de la existencia de raíces reales usando el discriminante:

$$ b^2-4ac = 1-4(4)(-7) = 1 + 112 = 113 > 0 $$

Por este motivo, el polinomio sí tiene raíces reales. Si el resultado del cálculo del discriminante hubiese sido menor que cero, nos habría indicado que el polinomio no posee raíces, dado que la ecuación \(f(x)=0\) no habría tenido solución. Se puede intentar factorizar mediante el tanteo, hallando dos números que sumados sean iguales a -1 y multiplicados sean iguales a -28. Esta labor es muy compleja si se quiere hallar por simple inspección, por lo tanto, se emplea la fórmula cuadrática para hallar las raíces reales del polinomio.

$$ x_{1,2} = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$

$$ x_{1,2} = \frac{1 \pm \sqrt{113}}{8} $$

Las soluciones son:

$$ x_{1} = \frac{1 + \sqrt{113}}{8} = 1.45$$

$$ x_{2} = \frac{1 - \sqrt{113}}{8} = -1.20$$

El polinomio factorizado requiere tener en cuenta las dos raíces halladas y el coeficiente de \(x^2\), así:

$$ f(x) = ax^2+bx+c = a \left( x - x_1 \right) \left( x - x_2 \right) $$

Finalmente:

$$ f(x) = 4x^2-x-7 = 4 \left[ x - \left( \frac{1 + \sqrt{113}}{8} \right) \right] \left[ x - \left( \frac{1 - \sqrt{113}}{8} \right) \right] $$

Se invita al lector a comprobar, desarrollando el producto, que se puede recobrar la forma original no factorizada de la función. Su gráfica se observa en la Figura 1.

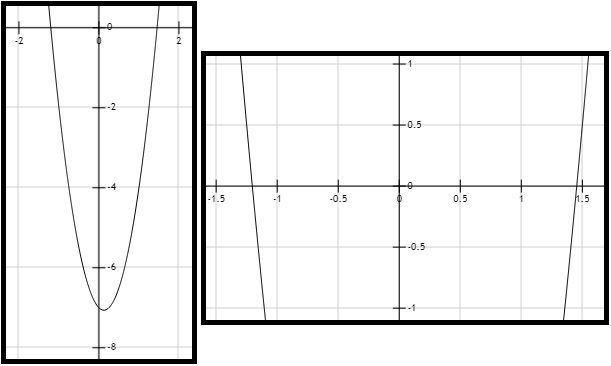
Figura 1. Gráfica de la función \( f(x) = 4x^2-x-7 \).