24. Hallar la forma simétrica de la ecuación de la recta que pasa por el punto \(P(1,-2,0)\), es paralela al plano \(\pi: 2x+y=3\) y es perpendicular a la recta

$$ \overleftrightarrow{r}: x=y-1=z $$

SOLUCIÓN

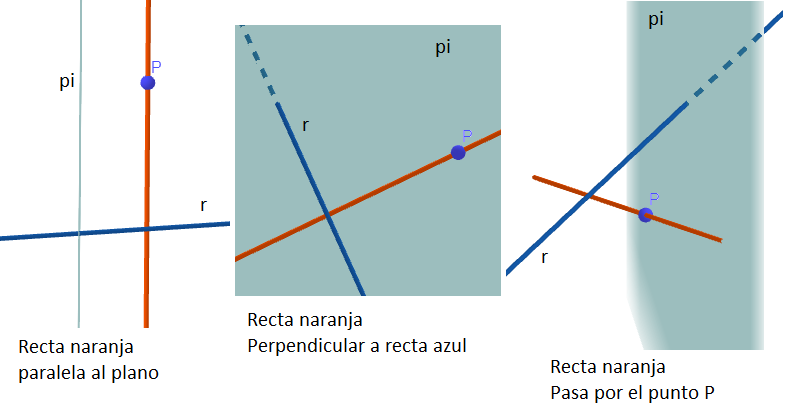
La forma simétrica de la ecuación de una recta que solicita el problema se escribe así:

$$ \frac{x-p_1}{d_1}=\frac{y-p_2}{d_2}=\frac{z-p_3}{d_3} $$

Un vector de componentes \( (p_1,p_2,p_3) \) se puede definir usando las coordenadas del punto \( P \). Sólo nos queda hallar un vector director de componentes \( (d_1,d_2,d_3) \) que sea paralelo al plano y perpendicular a la recta r. Si un vector es paralelo a un plano, entonces es perpendicular a su vector normal. Esto nos lleva a que el vector director buscado es perpendicular tanto dicho vector normal como al vector director de la recta r. Nuestro análisis se completa al pensar que un vector que es perpendicular a otros dos, se puede hallar usando un producto cruz entre esos dos vectores.

Hallemos el vector normal al plano \( \pi \). Sus componentes son los coeficientes de las variables x, y, z en la ecuación del plano. Es importante tener en cuenta que el problema no incluye a la variable z en la ecuación del plano, debido a que su coeficiente es cero, pero nada nos impediría escribirla como 2x+y+0z=3.

$$ \overrightarrow{n} = (2,1,0) $$

El vector director de la recta lo podemos hallar de los denominadores en la forma simétrica de la ecuación de la recta r, siempre y cuando ésta tenga la forma estándar. Miremos:

$$ \frac{x-0}{1}=\frac{y-1}{1}=\frac{z-0}{1} $$

El vector director es:

$$ d_r=(1,1,1) $$

Hallamos ahora el producto cruz entre estos dos vectores para calcular el vector director de la recta buscada:

$$ \overrightarrow{d} = \overrightarrow{n} \times \overrightarrow{d}_r = (2,1,0) \times (1,1,1) = (1,-2,1) $$

También pudimos haber realizado la operación en el otro orden, como dr x n, y habría resultado un vector (-1,2,-1), el cual es igual de útil. Finalmente, la forma simétrica de la ecuación de la recta buscada es:

$$ \frac{x-1}{1}=\frac{y+2}{-2}=\frac{z-0}{1} $$

Tuvimos en cuenta que el problema nos da el punto que pertenece a la recta, el cual es \(P(1,-2,0)\). Se podría dejar escrita así:

$$ x-1=\frac{y+2}{-2}=z $$

Si hubiésemos usado el otro vector director (-1,2,-1), hubiésemos obtenido otra forma igual de válida:

$$ 1-x=\frac{y+2}{2}=-z $$