- Visto: 11161
DIBUJO DE ENSAMBLES EXPLOSIVOS, EXPLOSIONADOS O EXPLOTADOS
En muchas instancias, las partes deben ser identificadas o ensambladas por personas poco calificadas en la lectura de dibujos de ingeniería. Ejemplos de esto se encuentran en la industria de reparación de aparatos, que se basa en dibujos de ensambles para efectuar composturas y para reordenar partes. Los dibujos de ensamble explosivo se usan mucho porque son fáciles de leer. Este tipo de dibujo de ensamble también se usa con frecuencia en compañías que manufacturan paquetes para ensamblar por las mismas personas, como son algunos tipos de muebles que se venden listos para armar.
DIBUJO DE ENSAMBLES EN SECCIÓN
Las vistas en corte, comúnmente llamadas secciones, se usan para mostrar detalles interiores demasiado complejos para mostrarse en vistas regulares, ya que contienen muchas líneas ocultas. Para los dibujos de montajes (como los que se muestran a continuación) las secciones indican diferencias entre partes y en el material. Las superficies expuestas o cortadas se identificarán mediante líneas de sección, también llamadas ashurado. Otro nombre que recibe el ashurado es rayado de sección. Las líneas ocultas que se encuentren detrás del plano de sección no se mostrarán a menos que sean necesarias para la claridad o para cotas de dimensionamiento. Con frecuencia una vista de corte reemplaza una vista regular.
Los dibujos seccionados se recomiendan para la mayoría de dibujos de ensamble, especialmente si son pequeños y detallados. Los dibujos seccionados para conjuntos tienen las siguientes características.
- Para partes adyacentes (piezas que están una al lado de la otra) las líneas de sección deben dibujarse en dirección opuesta, es decir, si un área posee líneas de sección con un ángulo de 45°, la pieza seccionada adyacente debe poseer líneas de sección con un ángulo de 45°+90°=135° ó -45°. En términos generales, los ángulos de secciones de piezas adyacentes deben ser lo suficientemente diferentes para poder distinguir una parte de la otra.
- El ashurado simbólico de corte (aquel donde el ashurado tiene un diseño específico según el tipo de material) se usa en dibujos de ensamble con un objetivo especial, como son ilustraciones de partes de catálogo, anuncios de ensamblaje, material de promoción o cuando sea conveniente distinguir los diferentes materiales.
- Piezas con geometrías de revolución como ejes y rodamientos, cuyos ejes se encuentran sobre el plano de corten, no se seccionan. Ver lista más completa de partes que no se seccionan en dibujos de montaje a continuación.
Partes mecánicas que NO se seccionan
En un dibujo de ensamble seccionado existen elementos que, a pesar de ser cortados por la línea de plano de corte, no se seccionan, es decir, no se dibujan líneas de sección en el área cortada. Los elementos, cuyos ejes caen sobre el plano de corte que no se seccionan son:
- Ejes.
- Tornillos.
- Tuercas.
- Arandelas.
- Pasadores.
- Varillas.
- Remaches.
- Cuñas (chavetas).
- Clavos.
- Rodamientos (en rodamientos de bolas éstas no se seccionan).
- Dientes de engranes.
- Partes sólidas similares.
A continuación se muestran ejemplos de dibujos de conjuntos seccionados. Ponga especial atención a aquellas piezas que contienen áreas en blanco, ya que corresponden a partes incluidas en la lista anterior que no seccionan aunque el plano de sección las corte.
Figura 1. Dibujos de ensamble o conjunto - Seccionado, isométrico y explotado - Rueda Carro de Corte. Tomada de [1].
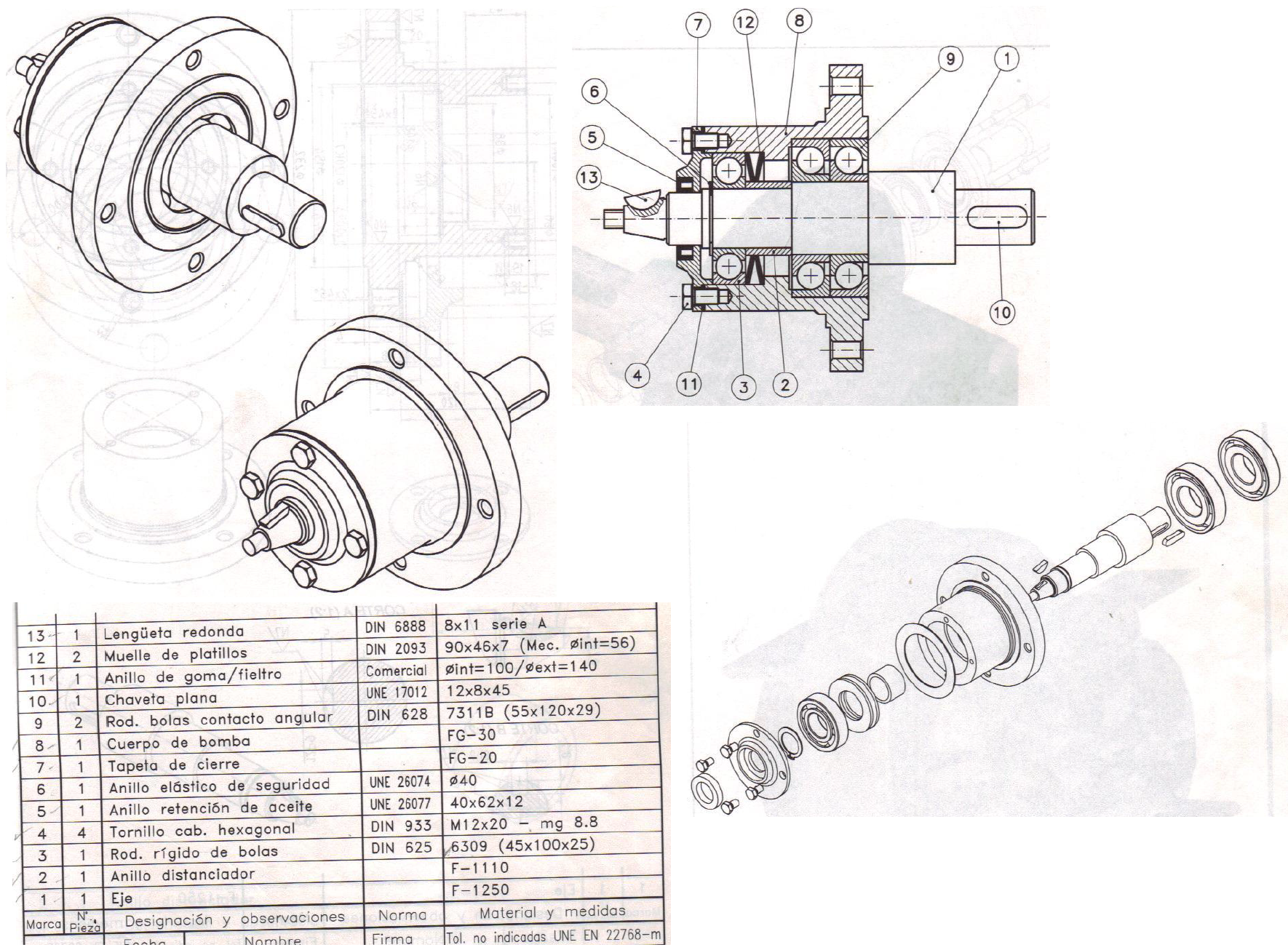Figura 2. Dibujos de ensamble o conjunto - Seccionado, isométrico y explotado - Bomba de pistones. Tomada de [1].
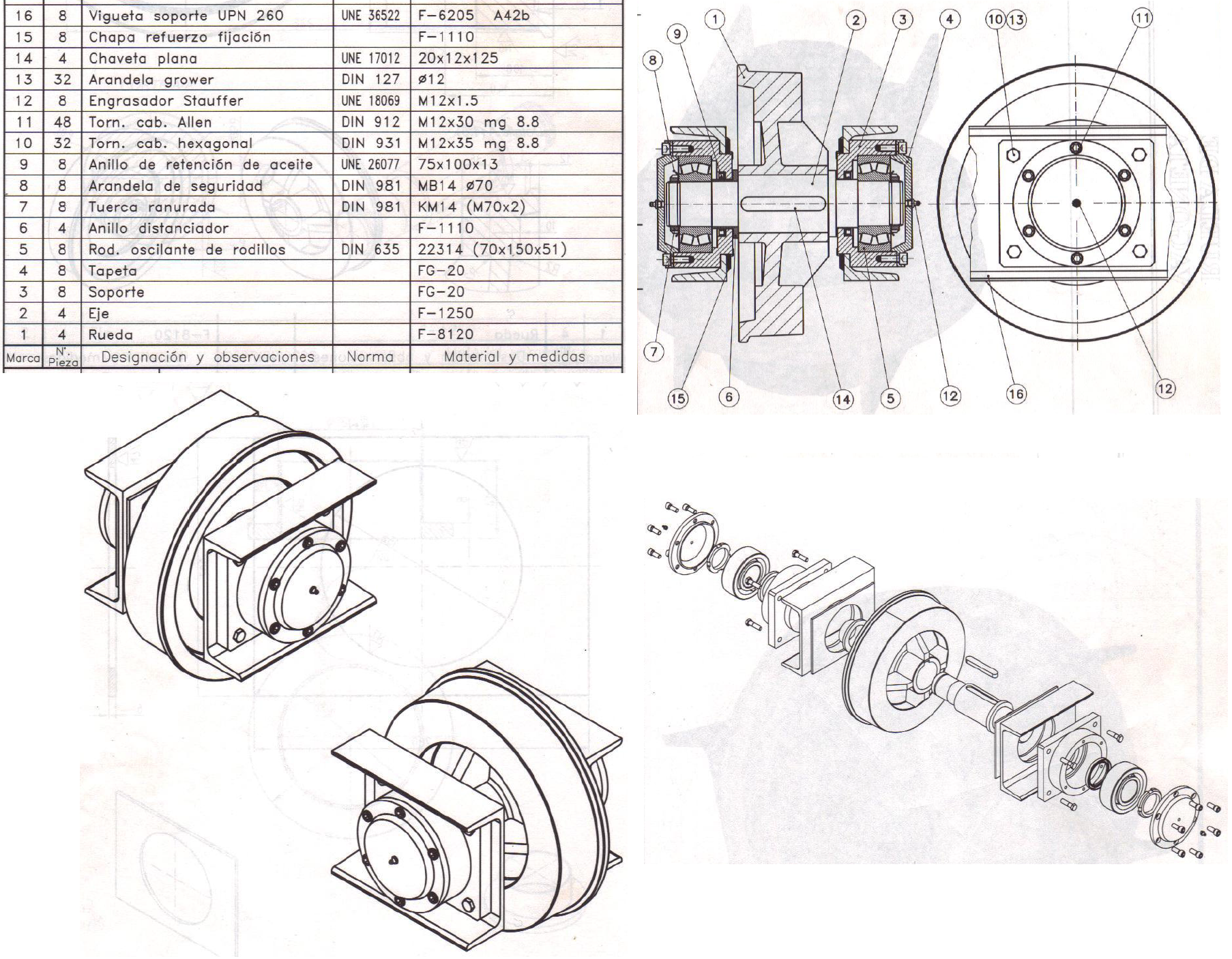Figura 3. Dibujos de ensamble o conjunto - Seccionado, isométrico y explotado - Rueda de vagoneta. Tomada de [1].
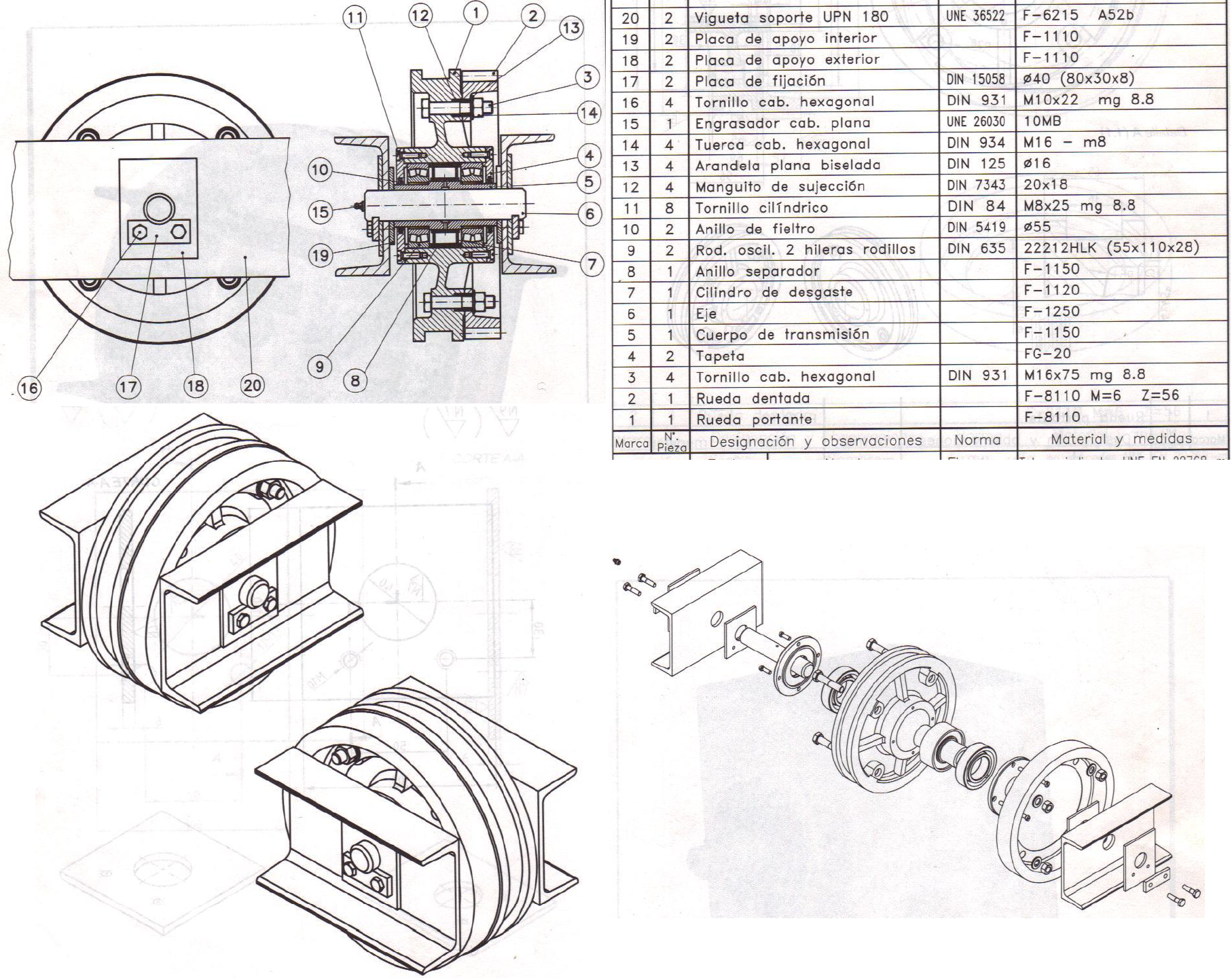Figura 4. Dibujos de ensamble o conjunto - Seccionado, isométrico y explotado - Rueda portante. Tomada de [1].
Figura 5. Dibujos de ensamble o conjunto - Seccionado, isométrico y explotado - Reductor de engranes. Tomada de [1].
Figura 6. Dibujos de ensamble o conjunto - Seccionado, isométrico y explotado - Útil de fijación. Tomada de [1].
Figura 7. Dibujos de ensamble o conjunto - Seccionado, isométrico y explotado - Tensor de polea. Tomada de [1].
Figura 8. Dibujos de ensamble o conjunto - Seccionado, isométrico y explotado - Rueda loca. Tomada de [1].
Figura 9. Dibujos de ensamble o conjunto - Seccionado, isométrico y explotado - Transmisión. Tomada de [1].
Figura 10. Dibujos de ensamble o conjunto - Seccionado, isométrico y explotado - Eje reductor. Tomada de [1].
Figura 11. Dibujos de ensamble o conjunto - Seccionado, isométrico y explotado - Rueda giro pórtico. Tomada de [1].
Figura 12. Dibujos de ensamble o conjunto - Seccionado, isométrico y explotado - Volante de transmisión. Tomada de [1].
Referencias
[1] AURIA A. José M., Ibáñez C. Pedro, Ubieto A. Pedro. Dibujo Industrial: conjuntos y despieces. Paraninfo, Thomson Learning. 2000.
Escribir comentario (1 Comentario)- Visto: 9380
DIBUJO DE EJES
Algunas características del dibujo de ejes para tener en cuenta son:
- La vista principal es una vista donde el eje se observa con su longitud horizontal sobre la hoja.
- Se puede proporcionar una vista lateral para indicar diámetros, aunque no es la práctica más común (ver Figura 1).
- Se puede proporcionar una vista isométrica.
- En la vista principal se pueden incluir dibujos seccionados parciales para mostrar el detalle de agujeros o chaveteros (ranuras que albergarán chavetas para transmitir movimiento) que de otra forma se observarían representados por líneas ocultas. Ver Figuras 1, 2, 4, 8, 10 y 11.
- Si el eje posee chaveteros, éstos se suelen dimensionar usando una vista con la verdadera forma de la ranura en la vista principal (ver Figuras 2, 3, 5, 6 y 9) y dibujos seccionados para mostrar las dimensiones de la sección transversal (ver Figuras 2, 3, 5, 6, 9, 11).
- En todos los dibujos de ejes se suelen incluir los símbolos y dimensiones de los acabados superficiales.
A continuación se proporcionan ejemplos de dibujo de ejes. Todos se hallan dibujados acorde con la norma de dibujo europea ISO, donde las vistas se hallan en el sistema de representación de primer ángulo diedro o primer cuadrante y el acotado sigue la norma ISO (mm). Todos los dibujos presentados a continuación son propiedad de los autores del texto (Auria et al, 2000) cuya referencia bibliográfica se halla al final de esta página.
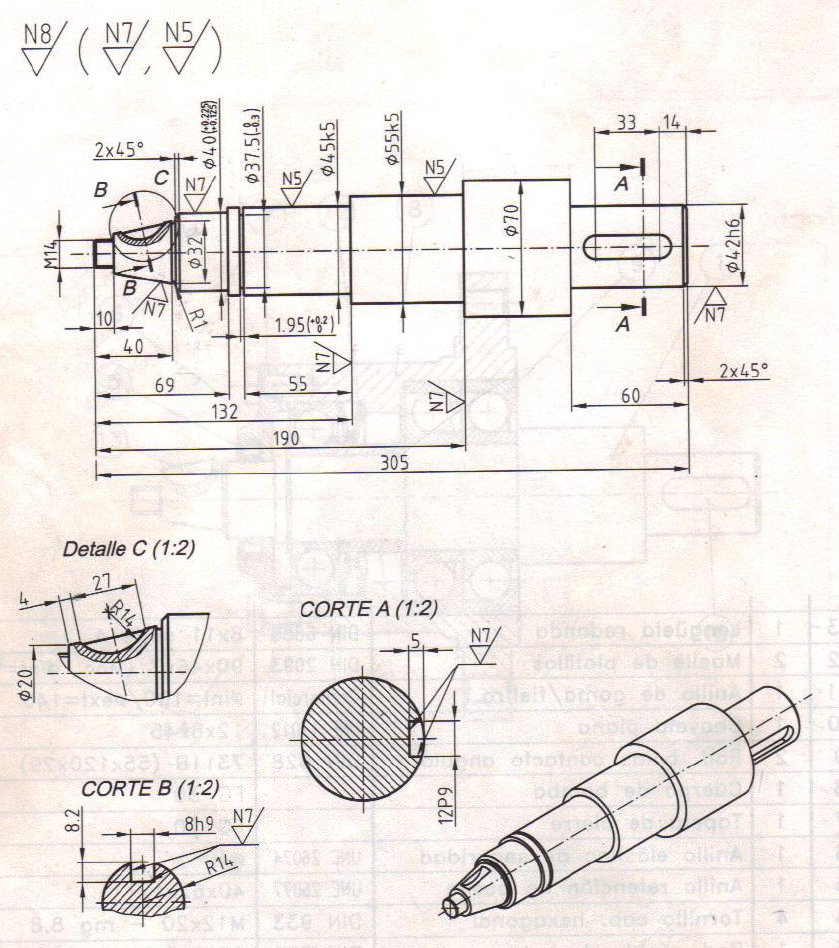
Figura 1. Eje con rosca y sección parcial dibujado con norma ISO primer cuadrante y unidades en mm. Imagen tomada de (Auria et al, 2000).
Figura 2. Eje con secciones y vista detallada dibujado bajo norma ISO primer cuadrante y unidades en mm. Imagen tomada de (Auria et al, 2000).
Figura 3. Eje con sección dibujado bajo norma ISO primer cuadrante y unidades en mm. Imagen tomada de (Auria et al, 2000).
Figura 4. Eje con sección parcial detallada dibujado bajo norma ISO primer cuadrante y unidades en mm. Imagen tomada de (Auria et al, 2000).
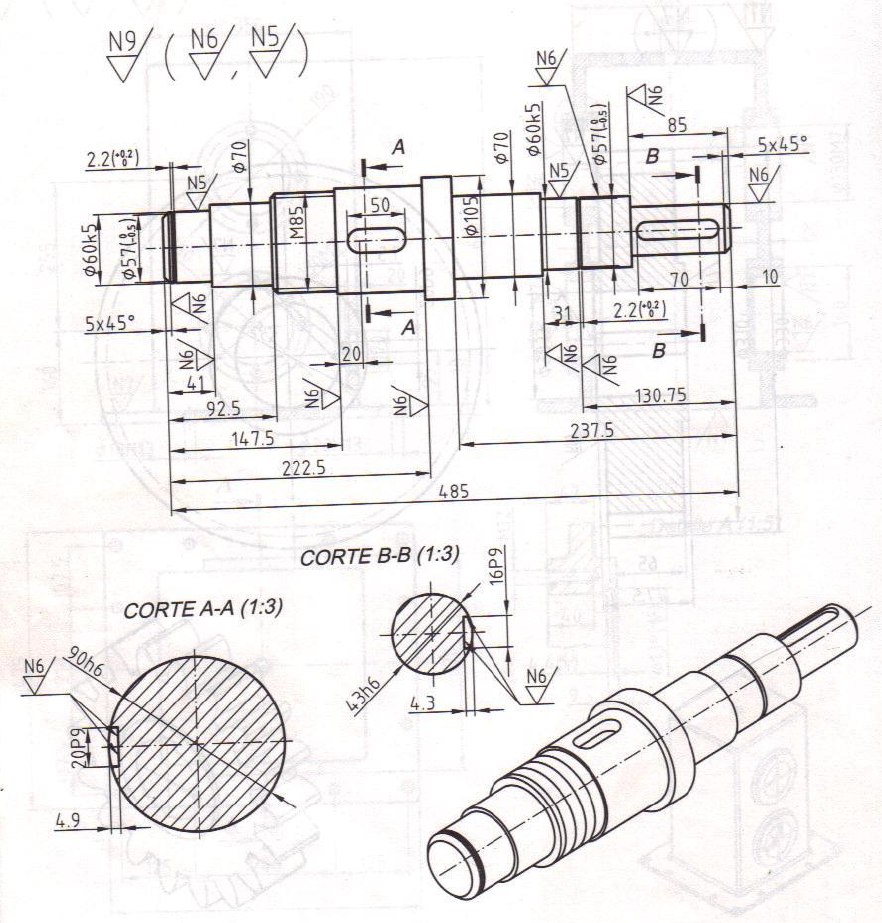
Figura 5. Eje con dos secciones para mostrar detalles de chaveteros dibujado bajo norma ISO primer cuadrante y unidades en mm. Imagen tomada de (Auria et al, 2000).
Figura 6. Eje roscado en extremos dibujado bajo norma ISO primer cuadrante y unidades en mm. Imagen tomada de (Auria et al, 2000).
Figura 7. Eje roscado en extremos dibujado bajo norma ISO primer cuadrante y unidades en mm. Imagen tomada de (Auria et al, 2000).
Figura 8. Eje con agujero roscado dibujado bajo norma ISO primer cuadrante y unidades en mm. Imagen tomada de (Auria et al, 2000).
Figura 9. Dibujo de eje con engrane y sección dibujado bajo norma ISO primer cuadrante y unidades en mm. Imagen tomada de (Auria et al, 2000).
Figura 10. Dibujo de eje con vistas seccionadas parciales dibujado bajo norma ISO primer cuadrante y unidades en mm. Imagen tomada de (Auria et al, 2000).
Figura 11. Dibujo de eje roscado con sección parcial dibujado bajo norma ISO primer cuadrante y unidades en mm. Imagen tomada de (Auria et al, 2000).
REFERENCIA BIBLIOGRÁFICA
AURIA Apilluelo, José M. Ibáñez, P. Ubieto, P. Dibujo industrial. Conjuntos y despieces. Paraninfo. Thomson Learning. Madrid, España. 2000.
Escribir comentario (1 Comentario)- Visto: 3857
En esta sección hallará ejercicios de dibujo de vistas seccionadas e isométricos seccionados a partir de vistas ortogonales dibujadas en el sistemas de representación de tercer cuadrante o tercer ángulo.
Taller de dibujo de vistas e isométricos en sección
El archivo siguiente contiene conjuntos de vistas ortogonales para ser usadas como ejercicios de interpretación de vistas para dibujo de isométricos. Las vistas están dispuestas de acuerdo al sistema de representación de tercer ángulo diedro o tercer cuadrante.
Escribir comentario (0 Comentarios)- Visto: 25764
|
Todos los dibujos asociados con este artículo se pueden hallar en el siguiente archivo para descarga ---> |
Dibujo_de_engrane_recto_V2022.zip |
TUTORIAL DIBUJO DE ENGRANES CON INVENTOR 2022
En este video se realiza el dibujo de un engrane en el entorno Ensamble usando el acelerador de componentes de Inventor. El engrane que se dibuja es un engrane de dientes rectos (Spur Gear). Se emplean varios comandos especiales para el dibujo del engrane, como son: - Export tooth shape en el entorno ensamble. - Get model sketches en el entorno de dibujo en el plano. También se utilizan iProperties de la parte para dibujar una tabla de datos de fresado y diligenciar el cuadro para título o cajetín adecuadamente y de forma automática. Se realiza también una vista seccionada del engranaje y se dibuja un alma, un cuñero y una maza. Todo el plano se realiza dibujando según orientaciones de la norma ANSI en pulgadas (in) y dibujos en el tercer ángulo diedro.
Los dibujos de trabajo de engranes rectos son relativamente simples. Generalmente consisten de dos vistas y una tabla de datos para el maquinado de los dientes. Como a los dientes se les da forma mediante fresadoras, no es necesario mostrar una vista detallada del perfil de los dientes ni tampoco una vista donde se observen todos ellos. La norma ANSI recomienda utilizar líneas fantasma para los círculos externos y de raíz y una línea de centro para el círculo primitivo. En la vista de corte, los círculos de raíz y externo se muestran como líneas continuas.
Las únicas diferencias en cuanto a terminología entre dibujos en engranes en pulgadas y en unidades métricas son los términos paso diametral y módulo.
PASO DIAMETRAL (engranes en pulgadas)
Para engranes en pulgadas se usa el término paso diametral en vez de módulo. El paso diametral es la relación del número de dientes a una longitud unitaria de diámetro de paso.
$$ \text{Paso diametral}=\frac{\text{Número de dientes}}{\text{Diámetro de paso}}=\frac{N}{PD} $$
MÓDULO (engranes en milímetros)
Es el término usado en engranes métricos. Es la longitud del diámetro de paso por diente medido en milímetros.
$$ \text{Módulo}=\frac{\text{Diámetro de paso}}{\text{Número de dientes}}=\frac{PD}{N} $$
De estas definiciones se desprende que el módulo es igual al recíproco del paso diametral y por lo tanto no es su equivalente dimensional métrico. Si se conoce el paso diametral, se puede obtener el módulo (use las mismas unidades para este cálculo). A continuación (mire la tabla más abajo) se resumen algunas (faltan varias) definiciones y fórmulas de engranes rectos para ángulos de presión de 14.5 o 20 grados. Por favor tomarla sólo como referencia. Para mayor confiabilidad en los datos y definiciones consultar bibliografía especializada en el tema.
Imagen tomada del sitio web de Autodesk: Engineer´s handbook | Inventor 2022.
Imagenes tomadas de Preview en el generador de engranes de Inventor.
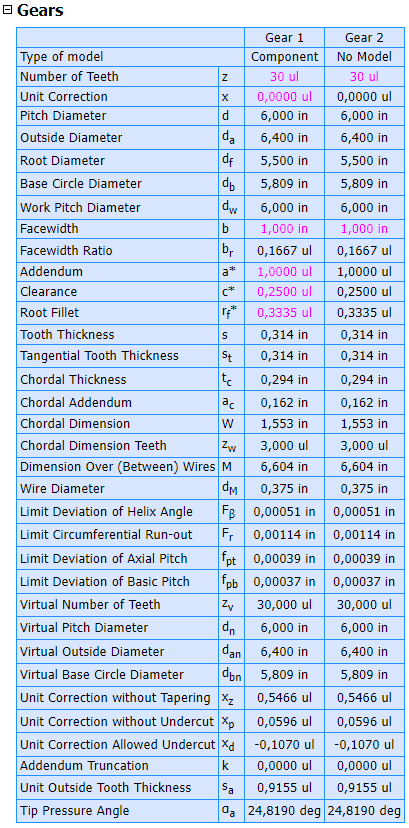
La siguiente tabla toma como referencia el texto Dibujo y Diseño en Ingeniería de Jensen, Helsel & Short, McGraw-Hill, 6a edición.
| Término y símbolo | Definición | Engranes métricos | Engranes en pulgadas | |
| 1. | Diámetro de paso-PD (Pitch Diameter). Letra d en la imagen. | Diámetro de un círculo imaginario en el cual se diseñan los dientes de un engrane. | PD=MDL*N | PD=N/DP |
| 2. | Número de dientes-N | Número de dientes del engrane. | Despejar de 1. | Despejar de 1. |
| 3. | Módulo-MDL | Longitud del diámetro de paso por diente. | Despejar de 1. MDL=1/DP (DP en mm). | No aplica (se usa sólo cuando se trabajan engranes en unidades métricas). |
| 4. | Paso diametral-DP (Diametral Pitch) | Relación igual al número de dientes de un engrane por cada pulgada de diámetro de paso. | No aplica (se usa sólo cuando se trabajan engranes en pulgadas). | Despejar de 1. DP=1/MDL (MDL en in). |
| 5. | Altura de la cabeza del diente-ADD (Addendum). Es ha en la imagen. | Distancia radial del círculo de paso a la parte superior del diente. | ADD=MDL | ADD=1/DP |
| 6. | Diámetro externo-OD. Es da en la imagen. | Diámetro total del engrane. | OD=PD+2*ADD=PD+2*MDL | OD=PD+2*ADD=(N+2)/DP |
| 7. | Diámetro de raíz-RD. Es df en la imagen. | Diámetro en la parte inferior del diente. | RD=PD-2*DED | RD=PD-2*DED |
| 8. | Profundidad de trabajo-WD | Profundidad de endentación de dos engranes. Suma de dos alturas de cabeza. | WD=2*ADD | WD=2*ADD |
| 9. | Ángulo de presión-PA. Es \(\alpha\) en la imagen. | Ángulo entre la dirección de presión de dientes en contacto y una línea tangente al círculo primitivo. | 14.5° o 20° |
14.5° o 20° |
| 10. | Distancia entre centros-DC | Distancia entre los ejes de los dos engranes. Se halla sumando los diámetros de paso (PD) de ambos engranes y dividiendo entre dos. | DC=(PD1+PD2)/2 |
DC=(PD1+PD2)/2 |
| 11. | Relación de transmisión-REL | Razón de valor más grande sobre más pequeño entre RPM, número de dientes o diámetros de paso de ambos engranes. | REL=RPM1/RPM2=N1/N2=PD1/PD2 |
REL=RPM1/RPM2=N1/N2=PD1/PD2 |
| 12. | Altura del diente-H. Es h en la imagen. | Distancia radial entre la raíz y la parte externa del diente. | H=(OD-RD)/2 |
H=(OD-RD)/2 |
Los módulos estándar para engranes métricos son 0.8, 1, 1.25, 1.5, 2.25, 3, 4, 6, 7, 8, 9, 10, 12 y 16 mm.
DIBUJO DE TRABAJO DE UN ENGRANE RECTO
Los siguientes son datos de fresado típicos para el maquinado de un engrane recto (ver tabla en imagen al inicio de este artículo):
- Número de dientes.
- Diámetro de paso.
- Módulo (si el engrane se halla en unidades métricas).
- Paso diametral (si el engrane se halla en unidades inglesas-pulgadas).
- Ángulo de presión.
- Profundidad total.
- Altura de diente desde cuerda.
- Espesor rectilíneo del diente.
- Espesor circular.
- Profundidad de trabajo.
- Diámetro de raíz.
- Diámetro externo.
- Altura del diente.
EJEMPLOS DE ENGRANES RECTOS SIMPLES EN PULGADAS
Use estos engranes individualmente para practicar su dibujo CAD y en el plano.
| Parámetro | Engrane 1 | Engrane 2 |
| Forma del diente | 14.5° | 20° |
| Diámetro de paso-PD | 6 in | - |
| Número de dientes | - | 50 |
| Paso diametral-DP | 5 | 5 |
| Ancho de cara | 1.00 in | 1.75 in |
| Espesor del alma | 0.4 in | - |
| Diámetro del eje | 1.1 in | 1.75 in |
| Maza | Diametro 1.9 x 1.5 longitud. | Diámetro 3 x 2.75 longitud. |
| Rayos | - | 0.6 in de espesor, 1.5 in de ancho, ahusados a 1.1 de ancho. |
| Material | Hierro maleable. | MI. |
EJEMPLOS DE ENGRANES RECTOS SIMPLES EN MILÍMETROS
Use estos engranes individualmente para practicar su dibujo CAD y en el plano.
| Parámetro | Engrane 1 | Engrane 2 |
| Forma del diente | 14.5° | 20° |
| Diámetro de paso-PD | 127 mm | - |
| Módulo | 6.35 mm | 6.35 mm |
| Número de dientes | - | 44 |
| Paso diametral-DP | - | - |
| Ancho de cara | 26 mm | 46 mm |
| Espesor del alma | 10 mm | - |
| Diámetro del eje | 28 mm | 45 mm |
| Maza | Diámetro 50 x 40 longitud | Diámetro 76 x 70.6 longitud |
| Rayos | - | 6 rayos de espesor 16 mm, 40 mm ancho, ahusados a 30 mm de ancho. |
| Material | Hierro maleable | Hierro maleable |
EJEMPLOS DE ENGRANES RECTOS ENDENTADOS EN PULGADAS
Use estos sistemas de engranes para practicar su dibujo CAD y en el plano.
| Parámetro | Piñón | Engrane |
| Forma del diente | 14.5° | 14.5° |
| Diámetro de paso-PD | - | - |
| Módulo | - | - |
| Número de dientes | 24 | 36 |
| Paso diametral-DP | - | - |
| Ancho de cara | - | 1.1 in |
| Espesor del alma | - | 0.4 in |
| Diámetro del eje | 1.1 in | 1.25 in |
| Maza | - | Diámetro 2.1 x 1.5 in long. |
| Rayos | - | - |
| Material | Acero | Hierro maleable |
| Distancia entre centros | 6 in | 6 in |
EJEMPLOS DE ENGRANES RECTOS ENDENTADOS EN MILÍMETROS
Use estos sistemas de engranes para practicar su dibujo CAD y en el plano.
| Parámetro | Piñón | Engrane |
| Forma del diente | 14.5° | 14.5° |
| Diámetro de paso-PD | - | - |
| Módulo | - | - |
| Número de dientes | 16 | 24 |
| Paso diametral-DP | - | - |
| Ancho de cara | - | 30 mm |
| Espesor del alma | - | 10 mm |
| Diámetro del eje | 30 mm | 32 mm |
| Maza | - | Diámetro 54 x 38 mm long. |
| Rayos | - | - |
| Material | Acero | Hierro maleable |
| Distancia entre centros | 127 mm | 127 mm |
DIBUJO DE ENGRANES RECTOS EN AUTODESK INVENTOR PROFESSIONAL
A continuación se mostrará la forma de realizar un plano básico de un engrane recto, desde su dibujo 3D hasta su dibujo en el plano con cotas y demás.
- PASO 1: DIBUJAR EL ENGRANE USANDO EL ACELERADOR DE COMPONENTES DE INVENTOR.
El engrane o tren de engranes se dibujará usando el acelerador de componentes de la pestaña Diseño en el entorno Ensamble (archivo .iam).
- PASO 2: EXPORTAR PIEZA CON FORMA DE DIENTE EN BOCETO.
En el arbol del modelo (model Browser) de la izquierda, buscar el tren de engranes generado usando el acelerador de componentes, luego ubicar el engrane que desea exportar y dele clic derecho y luego "Export tooth shape". Seleccione el componente correspondiente (piñón o rueda) y luego dé clic en OK. Se abrirá una ventana de un cilindro que representa el engrane, el cual contiene un boceto con la forma de un solo diente (útil para el dibujo en el plano). Guarde la pieza. Ésta será ahora su pieza de trabajo. Puede modificarla a su antojo y obtener de ella una vista simplificada del engrane (sin dientes, sólo un perfil de diente y líneas que representan diámetro externo, diámetro de paso y díametro de raíz).
- PASO 3: AGREGUE PARÁMETROS A LA PIEZA.
Al exportar, Inventor genera una lista de parámetros propios del engrane. Si falta alguno que sea importante para la lista de datos de fresado, inclúyalo en función de otros que si estén en la lista de parámetros. Cuidado con las unidades. Si estas no están bien escritas lo más probable es que los cálculos resulten incorrectos.
- PASO 4: AGREGUE UNA NUEVA REGLA PARA EL ENGRANE.
En la pestaña System, expanda "iProperties" (izquierda). Dé doble clic en "Custom". Aparecerá una línea de código en el espacio en blanco. Cambie el nombre de la propiedad "PropertyName" uno por uno para cada parámetro que quiera trasladar a las iProperties. Iguale cada línea a su respectivo parámetro. Quedará algo así:
iProperties.Value("Custom", "Module") = ModuleiProperties.Value("Custom", "NumberOfTeeth") = NumberOfTeeth
iProperties.Value("Custom", "PitchDiameter") = PitchDiameter
iProperties.Value("Custom", "TeethHeight") = TeethHeight
iProperties.Value("Custom", "RootDiameter") = RootDiameter
iProperties.Value("Custom", "HeadDiameter") = HeadDiameter
iProperties.Value("Custom", "PressureAngle") = PressureAngle
Lo que se hizo fue crear propiedades personalizadas, una por cada parámetro de la tabla de datos de fresado (arriba no están todos, es sólo un ejemplo).
- PASO 5: MOSTRAR BOCETOS DEL MODELO.
Crear una vista en el entorno plano (extensión .idw) del engrane (de la parte .ipt, no del ensamble) donde se observe de frente el engrane (como una circunferencia). Ubique el dibujo de la vista en el arbol de la izquierda (en el Browser), clic en más, luego clic derecho a la pieza .ipt del engrane. Luego clic en "Get Model Sketches". El perfil del diente del engrane y líneas que representan diámetros aparecerán. Cambie los tipos de línea. Use líneas ocultas para los diámetros de raíz y externo, y línea de eje para el diámetro de paso.
- PASO 6: CREAR TABLA DE DATOS DE FRESADO COMO SÍMBOLO
Expanda el icono de la biblioteca de símbolos "Drawing resources". En "Sketched Symbol" dé clic derecho y defina un nuevo símbolo, el cual será una tabla con los datos de fresado. Todas las "iProperties" estarán disponibles para que sean insertadas usando el comando Texto, al seleccionarlas e insertarlas. Ver "Custom Properties - Model" en el menú "Type".
- PASO 7: INSERTAR LA TABLA CREADA COMO SÍMBOLO.
Inserte la tabla buscando en el menú de símbolos del archivo vía "Insert Sketched Symbol".
CUÑAS O CHAVETAS CUADRADAS
Use el siguiente vínculo para leer un poco más acerca de las cuñas de este tipo: sobre las cuñas cuadradas. Use las siguientes tablas para seleccionar el tamaño adecuado de una cuña cuadrada en función del diámetro del eje.
| SISTEMA INGLÉS (PULGADAS) | ||
| Diámetro del eje | Tamaño nominal | |
| Desde | Hasta | W (ancho) y H (alto) (ambos) |
| .500 | .562 | .125 |
| .625 | .875 | .188 |
| .938 | 1.250 | .250 |
| 1.312 | 1.375 | .312 |
| 1.438 | 1.750 | .375 |
| 1.812 | 2.250 | .500 |
| 2.375 | 2.750 | .625 |
| 2.875 | 3.250 | .750 |
| 3.375 | 3.750 | .875 |
| 3.875 | 4.500 | 1.000 |
| SISTEMA MÉTRICO (MILÍMETROS) | ||
| Diámetro del eje | Tamaño nominal | |
| Desde | Hasta | W (ancho) y H (alto) (ambos) |
| 6 | 8 | 2 |
| 8 | 10 | 3 |
| 10 | 12 | 4 |
| 12 | 17 | 5 |
| 17 | 22 | 6 |
| 22 | 30 | 7 |
| 30 | 38 | 8 |
| 38 | 44 | 9 |
| 44 | 50 | 10 |
| 50 | 58 | 12 |
- Visto: 9373
Sistema diédrico
Representa geometrías del espacio sobre un plano reduciendo tres dimensiones a dos mediante una proyección ortogonal. Según el diccionario un diedro es un conjunto formado por dos semiplanos o caras con un borde común llamado arista. Si estos semiplanos se cortan perpendicularmente el diedro es rectángulo. Para generar vistas diedricas uno de los planos debe abatirse (desdoblarse) hasta ser coplanar con el segundo.
Las vistas o proyecciones se denominan alzada (el objeto se ve de frente), en planta (el objeto se ve desde arriba) y de perfil (el objeto se ve desde un lado). Este sistema es universalmente usado en arquitectura e ingeniería dado que las dimensiones paralelas a los planos de proyección se presentan en verdadera forma y tamaño.
Sistemas de representación
En todos los sistemas de representación, la proyección de los objetos se produce sobre las caras de un cubo, dentro del cual se imagina el objeto. Estas proyecciones se realizan mediante rayos proyectantes, que son líneas imaginarias que provienen de un punto exterior al cubo y pasan por todos los puntos del objeto. Al conjunto de todas las intersecciones de los rayos con un plano se le denomina como la proyección del objeto sobre ese plano.
Si el origen de los rayos proyectantes es un punto en el infinito, entonces todos los rayos serán paralelos entre sí, dando lugar a la proyección cilíndrica. Si dichos rayos resultan perpendiculares al plano de proyección la denominamos proyección cilíndrica ortogonal. Finalmente, si los rayos resultan oblicuos (inclinados) respecto al plano se denomina proyección cilíndrica oblicua. Si el origen de los rayos es un punto propio se tiene la proyección central o cónica.
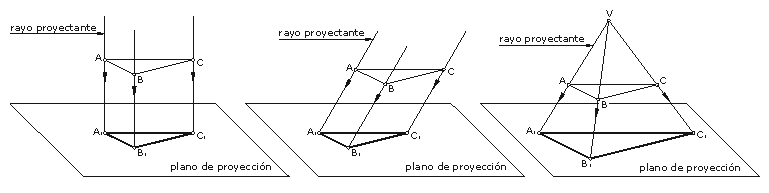
Figura 1. Proyección ortogonal (izquierda), oblicua (centro) y central o cónica (derecha).
Existen dos sistemas de representación. En ambos sistemas las proyecciones (representaciones 2D del objeto) son exactamente las mismas, pero las posiciones de las vistas son opuestas:
Proyección de primer ángulo (Sistema europeo)
Lo que el observador ve se proyecta alejándose de él. El orden es:
Observador - Objeto - Plano de proyección
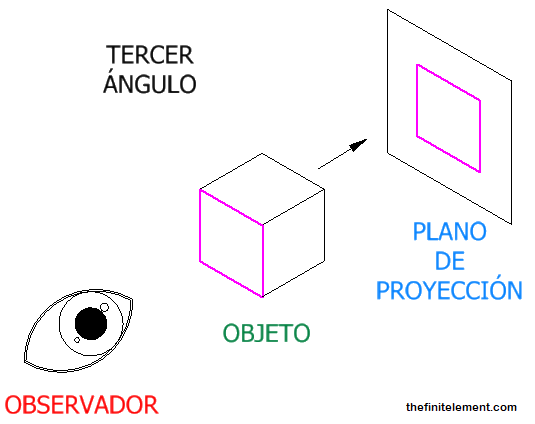
Proyección de tercer ángulo (Sistema americano)
Lo que el observador ve se proyecta hacia él. El orden es:
Observador - Plano de proyección - objeto
