En esta sección hallará definiciones y teoremas del tema de circunferencia de Geometría Euclidiana. Si desea acceder a algunos ejercicios resueltos del tema, puede visitar el siguiente vínculo:
| Ejercicios propuestos de circunferencias | Geometría Euclidiana |
DEFINICIONES DEL TEMA DE CIRCUNFERENCIA
CIRCUNFERENCIA: Dados un plano \(\pi\), un punto O en dicho plano y un número real positivo r, (r > 0), se llama “Circunferencia de centro O y radio r”, “C(O; r)”, al conjunto formado por todos los puntos P del plano \(\pi\), tales que OP = r.

RADIO: Segmento que une el centro con un punto de la circunferencia, por ejemplo: \(\overline{OA}\), \(\overline{OB}\), \(\overline{OC}\), \(\overline{OD}\), \(\overline{OE}\) y \(\overline{OF}\).
CUERDA: Segmento cuyos extremos son puntos de la circunferencia, por ejemplo: \(\overline{AB}\) y \(\overline{CD}\).
DIÁMETRO: Cuerda que pasa por el centro de la circunferencia, por ejemplo: \(\overline{CD}\).
ÁNGULO CENTRAL: Ángulo cuyo vértice es el centro de la circunferencia, por ejemplo: \(\angle EOF=\alpha\).
ARCO: Subconjunto de la circunferencia limitado por dos puntos de ella, por ejemplo: arco \(\overset{\LARGE\frown}{AB} \). Si son extremos de un diámetro, los arcos se llaman semicircunferencias, por ejemplo: \(\overset{\LARGE\frown}{CAD}\) y \(\overset{\LARGE\frown}{CED}\).
CIRCUNFERENCIAS CONCÉNTRICAS: Las que tienen el mismo centro.
TEOREMA: En una circunferencia, todos los radios son congruentes; todos los diámetros son congruentes; el diámetro es el doble del radio y el diámetro es la mayor cuerda.
POSICIÓN RELATIVA ENTRE UN PUNTO Y UNA CIRCUNFERENCIA
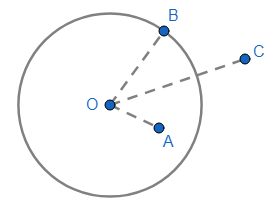
En un plano, dada una C(O; r) y un punto P:
1. P es INTERIOR a C(O; r), si OP < r.
2. P está SOBRE la C(O; r), si OP = r.
3. P es EXTERIOR a C(O; r), si OP > r.
DISTANCIA DE UN PUNTO A UNA CIRCUNFERENCIA
TEOREMA: Dada una circunferencia C(O; r) y dado un punto P en su plano, entonces los extremos del diámetro AB, contenido en la recta OP, son los puntos de la circunferencia que están a la menor y a la mayor distancia del punto dado.
La distancia del punto P a la C(O; r) es la distancia entre P y el extremo de dicho diámetro que esté más próximo a P, en la gráfica por ejemplo es PB.
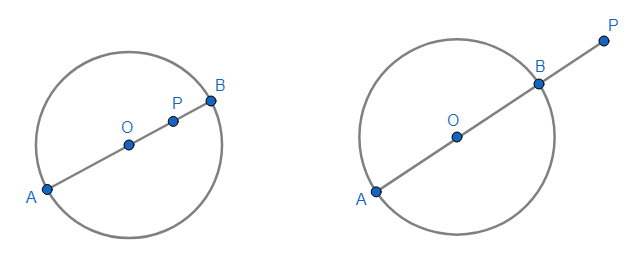
TEOREMA: Por tres puntos colineales no pasa ninguna circunferencia.
COROLARIO: Tres puntos de una circunferencia no pueden ser colineales. Intuitivamente “la circunferencia no tiene ningún tramo rectilíneo”.
CIRCUNFERENCIAS QUE PASAN POR TRES PUNTOS NO ALINEADOS DADOS
TEOREMA: Por tres puntos A, B y C no alineados, pasa una y sólo una circunferencia que tiene por centro el circuncentro O del triángulo ABC.
POSICIÓN RELATIVA ENTRE UNA RECTA Y UNA CIRCUNFERENCIA
1. Una recta es EXTERIOR a una circunferencia si no tiene puntos comunes con ella.
2. Una recta es TANGENTE a una circunferencia si tiene exactamente un punto común con ella, llamado punto de tangencia.
3. Una recta es SECANTE a una circunferencia si tiene exactamente dos puntos comunes con ella.
TEOREMA: Si una recta es tangente a una circunferencia entonces es perpendicular al radio que llega al punto de tangencia.
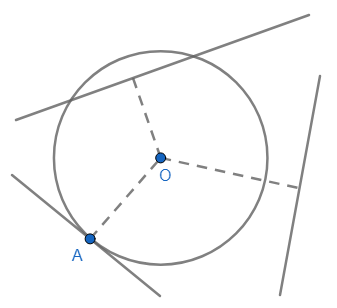
TEOREMA: Dadas una recta y una circunferencia de radio r, si d es la distancia del centro a la recta, entonces:
1. La recta es secante a la circunferencia si y sólo si d < r.
2. La recta es tangente a la circunferencia si y sólo si d = r.
3. La recta es exterior a la circunferencia si y sólo si d > r.
POSICIÓN RELATIVA ENTRE DOS CIRCUNFERENCIAS
Dos circunferencias son:
- EXTERIORES: Si todos los puntos de cada una de ellas son exteriores a la otra.
- TANGENTES EXTERIORES: Si tienen un punto común y los demás puntos de cada una de ellas son exteriores a la otra.
- SECANTES: Si tienen exactamente dos puntos comunes.
- TANGENTES INTERIORES: Si tienen un punto común y los demás puntos de una de ellas son interiores a la otra, entonces la primera es tangente interior a la segunda.
- INTERIORES: Si no tienen puntos comunes y todos los puntos de una de ellas son interiores a la otra, entonces la primera es interior a la segunda.
TEOREMA: Si dos circunferencias no concéntricas tienen un punto común exterior a la recta de los centros entonces son secantes y recíprocamente.
TEOREMA: Si dos circunferencias son secantes entonces la línea de sus centros es la mediatriz de su cuerda común y es la bisectriz de los ángulos centrales subtendidos por la cuerda.

TEOREMA: Si dos circunferencias son tangentes entonces los centros y su punto de tangencia son colineales y recíprocamente.
TEOREMA: Dadas dos circunferencias C(O; r) y C(O’; r’), entonces ellas son:
1. Exteriores: si y sólo si \(OO’ > r + r’ \).

2. Tangentes exteriores: si y sólo si \( OO’ = r + r’ \).

3. Secantes: si y sólo si \( |r-r'|< OO’ < r+r' \).

4. Tangentes interiores: si y sólo si \( OO’ = | r-r’| \).

5. Interiores: si y sólo si \( OO’ < | r-r'| \).

ARCOS Y CUERDAS
CIRCUNFERENCIAS CONGRUENTES: Dos circunferencias son congruentes si sus radios tienen igual medida.
ARCOS CONGRUENTES: Dos arcos de una misma circunferencia o de circunferencias congruentes son congruentes si subtienden ángulos centrales congruentes.
ARCOS DESIGUALES: Dos arcos de una misma circunferencia o de circunferencias congruentes son desiguales si subtienden ángulos centrales desiguales y será mayor el que subtienda mayor ángulo central.
MEDIDA ANGULAR DE UN ARCO: La medida angular de un arco es la medida del ángulo central que subtiende.
TEOREMA: En una misma circunferencia o en circunferencias congruentes:
- Dos ángulos centrales son congruentes sii subtienden cuerdas congruentes.
- Dos cuerdas son congruentes sii subtienden arcos congruentes.
- La menor de dos cuerdas desiguales subtiende un arco menor y un ángulo central menor y recíprocamente.
- Dos cuerdas congruentes equidistan del centro y recíprocamente.
- La mayor de dos cuerdas desiguales está más próxima al centro y recíprocamente.
PROPIEDADES DE UN DIÁMETRO PERPENDICULAR A UNA CUERDA
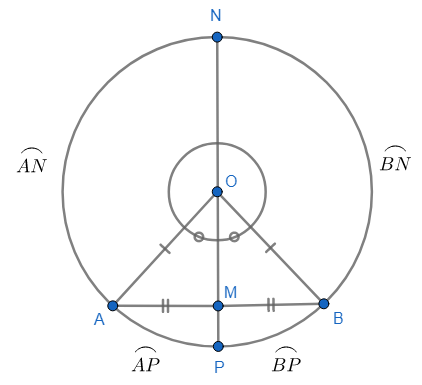
TEOREMA: Dada una cuerda, si otra cuerda secante a ella cumple dos de las siguientes propiedades entonces las cumple todas:
- Es diámetro: \(\overline{NP}\).
- Es perpendicular a la cuerda: \(\overline{NP} \perp \overline{AB}\).
- Pasa por el punto medio de la cuerda: \(M\) punto medio de \(\overline{AB}\).
- Pasa por el punto medio del arco menor: \(P\) punto medio de arco \(\overset{\LARGE\frown}{AB}\).
- Pasa por el punto medio del arco mayor: \(N\) punto medio de arco \(\overset{\LARGE\frown}{ANB}\).
- Es bisectriz del ángulo central que la cuerda subtiende: \(\overline{OP}\) bisectriz de \(\angle{AOB}\) y \(\overline{ON}\) bisectriz de \(\angle{AOB}\).
ARCOS Y PARALELAS
TEOREMA: Dos arcos o dos cuerdas comprendidos entre dos rectas paralelas son congruentes.
TEOREMA: (Criterio de paralelismo): Si en una circunferencia dos cuerdas o dos arcos son congruentes entonces sus extremos determinan un par de rectas paralelas.
ÁNGULOS RELACIONADOS CON LA CIRCUNFERENCIA
1. ÁNGULO INSCRITO: El vértice es un punto de la circunferencia y sus lados son dos semirrectas secantes a la circunferencia, por ejemplo el ángulo \(\angle{ABC}\).

2. ÁNGULO SEMIINSCRITO: El vértice es un punto de la circunferencia y sus lados son dos semirrectas una tangente y la otra secante a la circunferencia, por ejemplo el ángulo \(\angle{DEF}\).

3. ÁNGULO INTERIOR: El vértice es punto interior a la circunferencia y sus lados son dos semirrectas secantes a la circunferencia, por ejemplo el ángulo \(\angle{GHT}\).
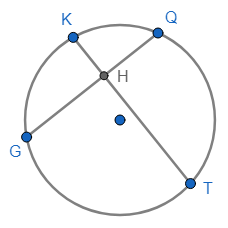
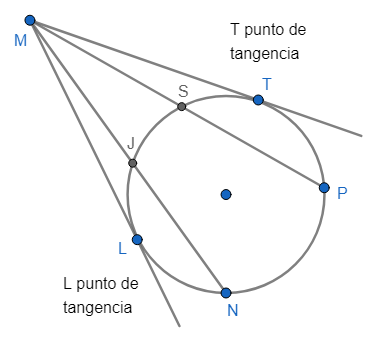
4. ÁNGULO EXTERIOR: El vértice es punto exterior a la circunferencia y sus lados son semirrectas tangentes y/o secantes a la circunferencia, por ejemplo los ángulos \(\angle{LMT}\), \(\angle{LMN}\) y \(\angle{LMP}\).
TEOREMAS: En una circunferencia, en medidas angulares:
1. Teorema del ángulo inscrito
Un ángulo inscrito mide la mitad del arco comprendido entre sus lados, por ejemplo:
$$ \angle{ABC}_{inscrito}=\frac{\overset{\LARGE\frown}{AC}}{2} $$

Tener en cuenta que la medida del arco AC es el valor del ángulo central subtendido por el arco AC.
Corolarios del teorema del ángulo inscrito
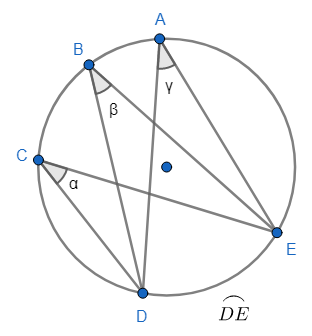
Corolario 1
Todos los ángulos inscritos que subtienden el mismo arco son congruentes. Entonces, si \(\alpha\), \(\beta\) y \(\gamma\) son ángulos inscritos que subtienden el mismo arco, se cumple que:
$$ \alpha=\beta=\gamma=\frac{\overset{\LARGE\frown}{DE}}{2} $$
Corolario 2
Todos los ángulos inscritos en una semicircunferencia son rectos. Dicho esto, si \(\alpha\), \(\beta\) y \(\gamma\) son ángulos inscritos en una semicircunferencia, siendo \(\overline{AB}\) diámetro, entonces se cumple que:
$$ \alpha = \beta = \gamma = \frac{\overset{\LARGE\frown}{AB}}{2} = \frac{180°}{2} = 90° $$

2. Teorema del ángulo semiinscrito
Un ángulo semiinscrito mide la mitad del arco comprendido entre sus lados, por ejemplo:
$$ \angle{DEF}_{semiinscrito} = \frac{\overset{\LARGE\frown}{DE}}{2}$$

3. Teorema del ángulo interior
Un ángulo interior mide la semisuma del arco comprendido entre sus lados y el arco comprendido entre las prolongaciones de ellos, por ejemplo:
$$ \angle{GHT}_{interior} =\angle{KHQ}_{interior} =\frac{\overset{\LARGE\frown}{GT}+\overset{\LARGE\frown}{KQ}}{2}$$
$$ \angle{KHG}_{interior} =\angle{QHT}_{interior} =\frac{\overset{\LARGE\frown}{KG}+\overset{\LARGE\frown}{QT}}{2}$$

4. Teorema del ángulo exterior
Un ángulo exterior mide la semidiferencia de los arcos mayor y menor comprendidos entre sus lados. Tres posibilidades de aplicación del teorema dependen de cómo se forma el ángulo exterior, es decir: a) con dos lados tangentes, b) con un lado tangente y uno secante y c) con dos lados sectantes a la circunferencia.
$$ \angle{LMT}= \frac{\overset{\LARGE\frown}{LNT}-\overset{\LARGE\frown}{LJT}}{2}$$
$$ \angle{LMN}= \frac{\overset{\LARGE\frown}{LN}-\overset{\LARGE\frown}{LJ}}{2} $$
$$ \angle{NMP}= \frac{\overset{\LARGE\frown}{NP}-\overset{\LARGE\frown}{JS}}{2} $$

ARCO CAPAZ (Lugar Geométrico)
TEOREMA: Dado un segmento \(\overline{AB}\) y dado un ángulo, \(0° < \alpha < 180°\), entonces existen dos arcos de extremos A y B, (sobre circunferencias congruentes y simétricas con respecto a la recta AB), tales que la unión de dichos arcos, excepto los puntos A y B, forman el lugar geométrico de los puntos P del plano, para los cuales \( \angle{APB} = \alpha\).
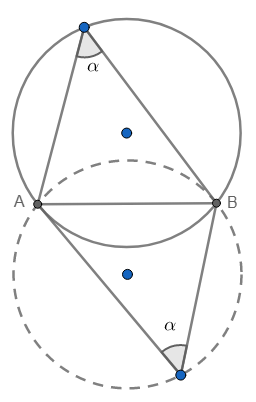
ARCO CAPAZ: Dado un segmento AB y dado un ángulo \(\alpha\), tal que \(0° < \alpha < 180°\), el ''arco capaz del segmento \(\overline{AB}\) bajo el ángulo \(\alpha\)'', es cada uno de los arcos a los que se refiere el teorema anterior.
TEOREMA: El arco capaz de un segmento, bajo 90° es la semicircunferencia que le tiene por diámetro.
PROPIEDADES DE LAS RECTAS TANGENTES DESDE UN PUNTO EXTERIOR
TEOREMA: Sean PA y PB los segmentos tangentes a una circunferencia trazados desde un punto P exterior a ella, (A y B puntos de tangencia), entonces:

1. Las tangentes son congruentes \(PA = PB\).
2. \(\overline{OP}\) es bisectriz del ángulo \(\angle{AOB}\) y del ángulo \(\angle{APB}\).
3. \(\angle{AOB}=\angle{TPB}\) (exterior) del cuadrilátero \(PAOB\).





Comentarios potenciados por CComment