Solución de cuadriláteros con Autodesk Inventor

Si desea conocer una herramienta de dibujo avanzada para solucionar problemas de Geometría Euclidiana, lo invito a mirar un video tutorial para aprovechar esta poderosa herramienta.

Vea el artículo aquí: Solución de problemas de cuadriláteros con Inventor

DEFINICIONES

PARALELOGRAMO: Es un cuadrilátero cuyos lados opuestos son paralelos.

ABCD es un paralelogramo luego, por definición, \(\overline{AB} \parallel \overline{DC}\) y \(\overline{AD} \parallel \overline{BC}\).

RECTÁNGULO: Es un cuadrilátero con sus cuatro ángulos interiores congruentes.

ABCD es un rectángulo luego, por definición, \(\angle A \cong \angle B \cong \angle C \cong \angle D \).

ROMBO: Es un cuadrilátero con sus cuatro lados congruentes.

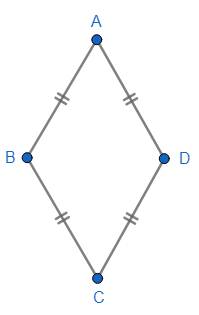
ABCD es un rombo luego, por definición, \( \overline{AB} \cong \overline{BC} \cong \overline{CD} \cong \overline{DA} \).

CUADRADO: Es un cuadrilátero con sus cuatro ángulos interiores congruentes y cuatro lados congruentes, es decir si es rectángulo y rombo a la vez.

ABCD es un cuadrado luego, por definición, \(\angle A \cong \angle B \cong \angle C \cong \angle D\) y \(\overline{AB} \cong \overline{BC} \cong \overline{CD} \cong \overline{DA}\).

TRAPECIO: Es un cuadrilátero convexo con un par de lados paralelos y el otro par no paralelos.

ABCD es un trapecio luego, por definición, \(\overline{AB} \parallel \overline{DC}\) y \(\overline{AD} \nparallel \overline{BC}\).

TRAPECIO ISÓSCELES: Es un trapecio que tiene congruentes los lados no paralelos.

ABCD es un trapecio isósceles luego, por definición, ABCD es un trapecio y \(\overline{AD} \cong \overline{BC}\).

TRAPECIO RECTÁNGULO: Es un trapecio que tiene un ángulo recto.

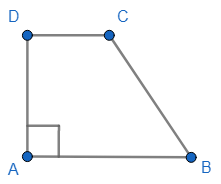
ABCD es un trapecio rectángulo luego, por definición, ABCD es un trapecio y \(\angle A = 90°\).

TRAPEZOIDE: Es un cuadrilátero con ningún par de lados paralelos.

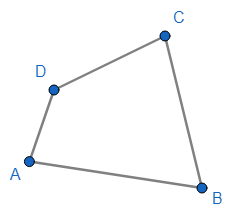
ABCD es un trapezoide luego, por definición, \(\overline{AB} \nparallel \overline{CD}\) y \(\overline{AD} \nparallel \overline{BC}\).

PROPIEDADES DEL PARALELOGRAMO

TEOREMA: En todo paralelogramo se cumplen las siguientes propiedades:

1. Los lados opuestos son respectivamente paralelos.
2. Los lados opuestos son respectivamente congruentes.
3. Los ángulos opuestos son respectivamente congruentes.
4. Las diagonales se cortan en su punto medio.

CRITERIOS DE PARALELOGRAMO

TEOREMA: Si en un cuadrilátero convexo se cumple cualquiera de las siguientes propiedades entonces es un paralelogramo:

1. 1. Los lados opuestos son paralelos.
2. Los lados opuestos son respectivamente congruentes.
3. Un par de lados opuestos son paralelos y congruentes.
4. Los ángulos opuestos son respectivamente congruentes.
5. Las diagonales se cortan en su punto medio.

PROPIEDADES DEL RECTÁNGULO

TEOREMA: En todo rectángulo se cumplen las siguientes propiedades:

1. Los cuatro ángulos interiores son rectos.
2. El rectángulo es paralelogramo.
3. Las diagonales son congruentes.

CRITERIOS DE RECTÁNGULO

TEOREMA: Si en un cuadrilátero convexo se cumple cualquiera de las siguientes propiedades entonces es un rectángulo:

1. Tiene tres ángulos rectos.
2. Es un paralelogramo con un ángulo recto.
3. Las diagonales son congruentes y se cortan en su punto medio.

PROPIEDADES DEL ROMBO

TEOREMA: En todo rombo se cumplen las siguientes propiedades:

1. Los cuatro lados son congruentes.
2. Es paralelogramo.
3. Las diagonales son perpendiculares.
4. Cada diagonal es bisectriz.

CRITERIOS DE ROMBO

TEOREMA: Si en un cuadrilátero convexo se cumple cualquiera de las siguientes propiedades entonces es un rombo:

1. Los cuatro lados son congruentes.
2. Es un paralelogramo con dos lados consecutivos congruentes.
3. Las diagonales son perpendiculares y se cortan en su punto medio.
4. Cada diagonal es bisectriz.

PROPIEDADES DEL CUADRADO

TEOREMA: Todo cuadrado es paralelogramo, rectángulo y rombo y por lo tanto cumple todas las propiedades de éstos.

CRITERIOS DE CUADRADO

TEOREMA: Si en un cuadrilátero convexo se cumple cualquiera de las siguientes propiedades entonces es un cuadrado:

1. Es rectángulo y rombo.
2. Es un rectángulo con dos lados consecutivos congruentes.
3. Es un rombo con un ángulo recto.
4. Las diagonales son perpendiculares, congruentes y se cortan en su punto medio.

PROPIEDADES DEL TRAPECIO

TEOREMA: En todo trapecio los lados paralelos son desiguales.

En un trapecio, los lados paralelos se llaman BASE MAYOR y BASE MENOR; el segmento que une los puntos medios de los lados no paralelos se llama la BASE MEDIA; la distancia entre las bases es la ALTURA.

TEOREMA: En un trapecio, los ángulos adyacentes a cada uno de los lados no paralelos son suplementarios.

Teorema de la base media de un trapecio

La base media de un trapecio es paralela a las bases y es congruente con la semisuma de las bases mayor y menor, es decir:

$$ MN = \frac{AB+DC}{2} $$

Demostración: Teorema de base media de un trapecio

TEOREMA: El segmento que une los puntos medios de las diagonales de un trapecio está contenido en la base media y es congruente con la semidiferencia entre las bases mayor y menor.

PROPIEDADES DEL TRAPECIO ISÓSCELES

TEOREMA: En todo trapecio isósceles se cumplen las siguientes propiedades:

1. Los lados no paralelos son congruentes.
2. Los ángulos adyacentes a cada una de sus bases son congruentes.
3. Los ángulos opuestos son suplementarios.
4. Las diagonales son congruentes.
5. Las mediatrices de las bases coinciden, y las mediatrices de los cuatro lados concurren.

Teorema de ángulos congruentes y suplementarios en un trapecio isósceles

En todo trapecio isósceles se cumple que los ángulos adyacentes a cada una de sus bases son congruentes y que los ángulos opuestos son suplementarios, es decir:

$$ \angle A = \angle B $$

$$ \angle D = \angle C $$

$$ \angle A + \angle D = \angle B + \angle C = 180° $$

Demostración: Teorema de ángulos congruentes y suplementarios en trapecio isósceles

CRITERIOS DE TRAPECIO ISÓSCELES

TEOREMA: Si en un trapecio se cumple cualquiera de las siguientes propiedades entonces es isósceles:

1. Los lados no paralelos son congruentes.
2. Los ángulos adyacentes a una de las bases son congruentes.
3. Un par de ángulos opuestos son suplementarios.
4. Las diagonales son congruentes.
5. Las mediatrices de las bases coinciden.