DEFINICIÓN DE TRIÁNGULO
Un triángulo es un polígono de tres vértices. Tiene tres lados, tres ángulos interiores y tres ángulos exteriores. Si los vértices son A, B y C lo denotamos \(\triangle ABC\).
CLASIFICACIÓN SEGÚN SUS LADOS
Un triángulo es:
- ESCALENO: si tiene sus tres lados desiguales.
- ISÓSCELES: si tiene por lo menos un par de lados congruentes. Si \(\overline{AB} \cong \overline{AC}\) entonces se dice que el \(\triangle ABC\) es isósceles de base \(\overline{BC}\).
- EQUILÁTERO: si tiene sus tres lados congruentes.
CLASIFICACIÓN SEGÚN SUS ÁNGULOS
Un triángulo es:
- ACUTÁNGULO: Si tiene los tres ángulos agudos.
- RECTÁNGULO: Si tiene un ángulo recto. El lado opuesto al ángulo recto es la hipotenusa y los lados que lo forman son los catetos.
- OBTUSÁNGULO: Si tiene un ángulo obtuso.
- EQUIÁNGULO: Si tiene los tres ángulos congruentes.
TEOREMA
Todo triángulo equilátero es isósceles. El recíproco es falso.
LÍNEAS NOTABLES EN EL TRIÁNGULO
- MEDIANA: es el segmento que une un vértice con el punto medio de su lado opuesto. Por ejemplo, el segmento \(\overline{AM}\). Todo triángulo tiene tres medianas, las cuales se intersecan en el baricentro.

- ALTURA: es la perpendicular trazada desde un vértice a su lado opuesto o a su prolongación. En la figura de la izquierda la altura \(\overline{AH}\) es interior al triángulo \(\triangle ABC\), mientras que en la figura de la derecha la altura \(\overline{AH}\) es exterior al triángulo, y se forma entre el vértice \(A\) y la prolongación del lado \(\overline{CB}\). Todo triángulo tiene tres alturas, las cuales se intersecan en el ortocentro.

- MEDIATRIZ: es la perpendicular que pasa por el punto medio de un lado. Por ejemplo, el segmento \(\overline{MN}\). Todo triángulo tiene tres mediatrices, las cuales se intersecan en el circuncentro.
- BISECTRIZ: divide el ángulo interior o exteriores de cada vértice en dos ángulos congruentes. Por ejemplo, el segmento \(\overline{AD}\) divide al ángulo interior \(B\hat{A}C\) en dos ángulos con igual medida \(\beta\). El ángulo exterior que se forma en \(A\) también posee una bisectriz exterior que divide al ángulo exterior en dos ángulos congruentes \(\theta\). Recordar que el ángulo exterior de un triángulo se forma entre un lado y la prolongación de uno de los dos lados restantes. Todo triángulo tiene tres bisectrices interiores y tres bisectrices exteriores. Las tres bisectrices interiores se intersecan en el incentro.

CONGRUENCIA DE TRIÁNGULOS
DEFINICIÓN: dos triángulos son congruentes si tienen sus tres lados respectivamente congruentes y sus tres ángulos respectivamente congruentes. Dos elementos respectivamente congruentes son homólogos. Se puede escribir: LsHs (Lados Homólogos) y AsHs (Ángulos Homólogos). Entonces:
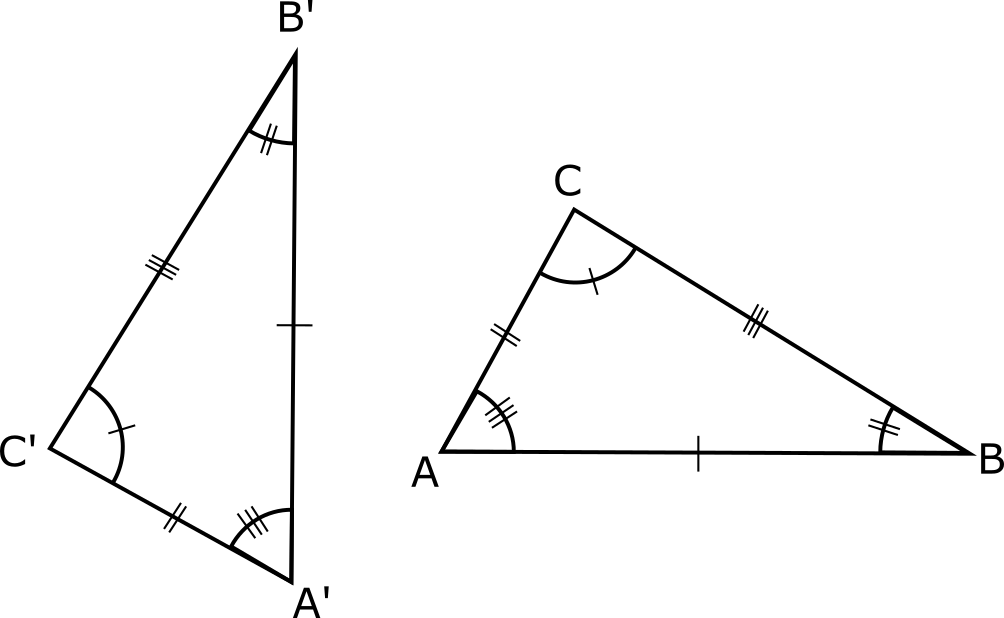
$$\triangle ABC \cong \triangle A'B'C'$$
$$\text{Sí y sólo si se cumplen las seis condiciones siguientes:}$$
$$ 1.~\overline{AB} \cong \overline{A'B'} $$
$$ 2.~\overline{BC} \cong \overline{B'C'} $$
$$ 3.~\overline{AC} \cong \overline{A'C'} $$
$$ 4.~ \hat{A} \cong \hat{A'} $$
$$ 5.~ \hat{B} \cong \hat{B'} $$
$$ 6.~ \hat{C} \cong \hat{C'} $$
CRITERIOS DE CONGRUENCIA DE TRIÁNGULOS
1. CRITERIO LADO-ÁNGULO-LADO (LAL)
Dos triángulos son congruentes si tienen un ángulo congruente formado por lados respectivamente congruentes.
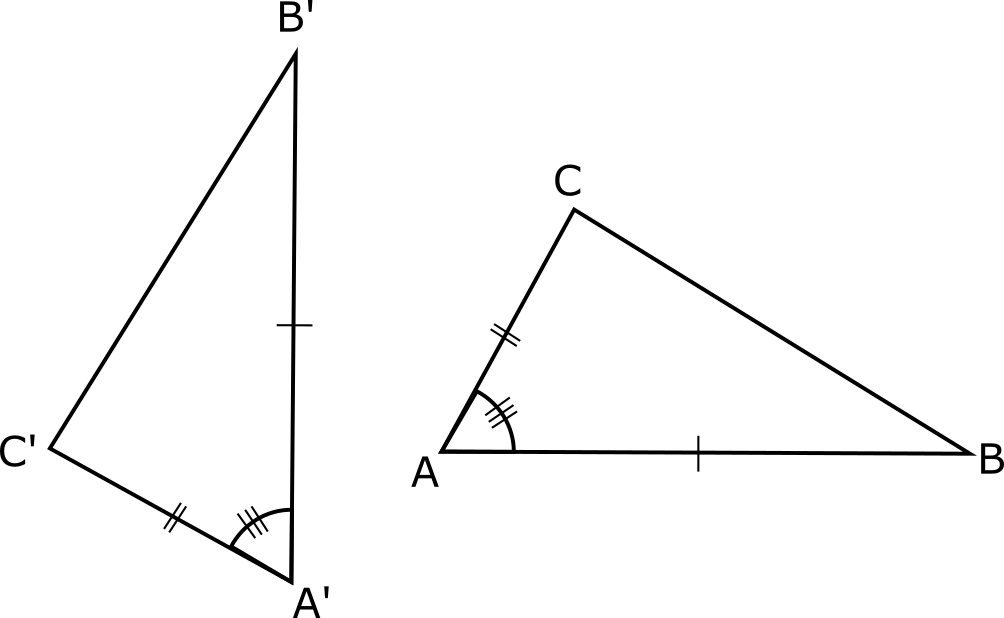
$$\triangle ABC \cong \triangle A'B'C'$$
$$\text{Sí y sólo si se cumplen las tres condiciones siguientes, en ese orden:}$$
$$ 1.~\overline{AB} \cong \overline{A'B'} $$
$$ 4.~ \hat{A} \cong \hat{A'} $$
$$ 3.~\overline{AC} \cong \overline{A'C'} $$
COROLARIOS
- En todo triángulo isósceles los ángulos opuestos a los lados congruentes son congruentes.
- Todo triángulo equilátero es equiángulo.
- En todo triángulo isósceles, la bisectriz del ángulo opuesto a la base también es mediana, altura y mediatriz con respecto a la base.
- Por un punto exterior a una recta pasa una y sólo una perpendicular a ella.
- En todo triángulo, cada ángulo exterior es mayor que cualquiera de los dos ángulos interiores no adyacentes.
- Todo triángulo tiene por lo menos dos ángulos agudos.
2. CRITERIO ÁNGULO-LADO-ÁNGULO (ALA)
Dos triángulos son congruentes si tienen respectivamente congruentes dos ángulos y el lado común a ellos.

$$\triangle ABC \cong \triangle A'B'C'$$
$$\text{Sí y sólo si se cumplen las tres condiciones siguientes, en ese orden:}$$
$$ 4.~ \hat{A} \cong \hat{A'} $$
$$ 3.~\overline{AC} \cong \overline{A'C'} $$
$$ 6.~ \hat{C} \cong \hat{C'} $$
COROLARIOS
- Si un triángulo tiene dos ángulos congruentes entonces es isósceles.
- Todo triángulo equiángulo es equilátero.
3. CRITERIO LADO-LADO-LADO (LLL)
Dos triángulos son congruentes si tienen sus tres lados respectivamente congruentes.
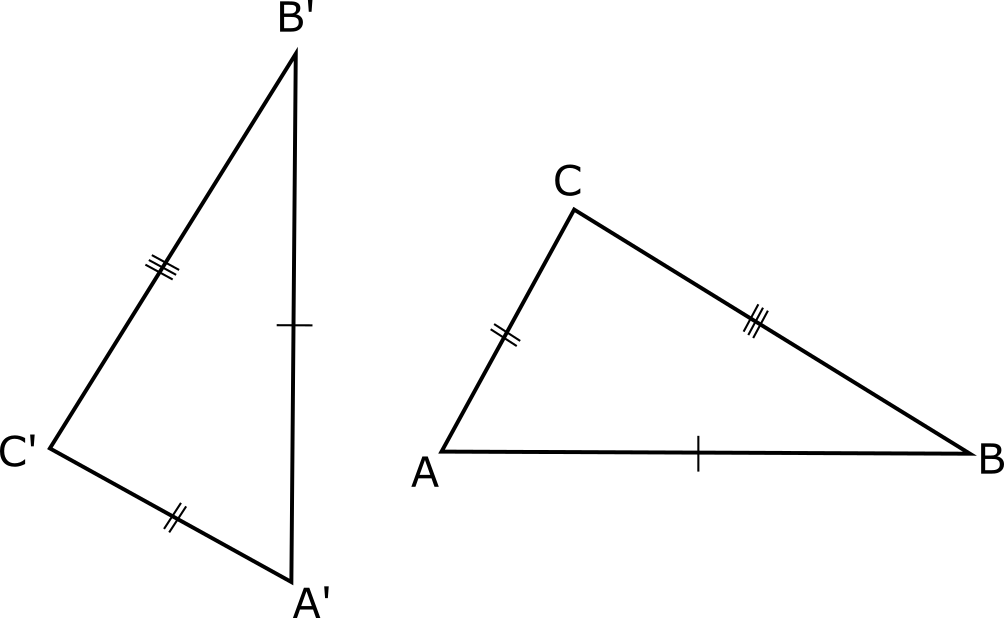
$$\triangle ABC \cong \triangle A'B'C'$$
$$\text{Sí y sólo si se cumplen las tres condiciones siguientes:}$$
$$ 1.~\overline{AB} \cong \overline{A'B'} $$
$$ 2.~\overline{BC} \cong \overline{B'C'} $$
$$ 3.~\overline{AC} \cong \overline{A'C'} $$
4. CRITERIO ÁNGULO-ÁNGULO-LADO (A1A2L1)
Dos triángulos son congruentes si tienen dos ángulos respectivamente congruentes y el lado opuesto a uno de ellos congruente.
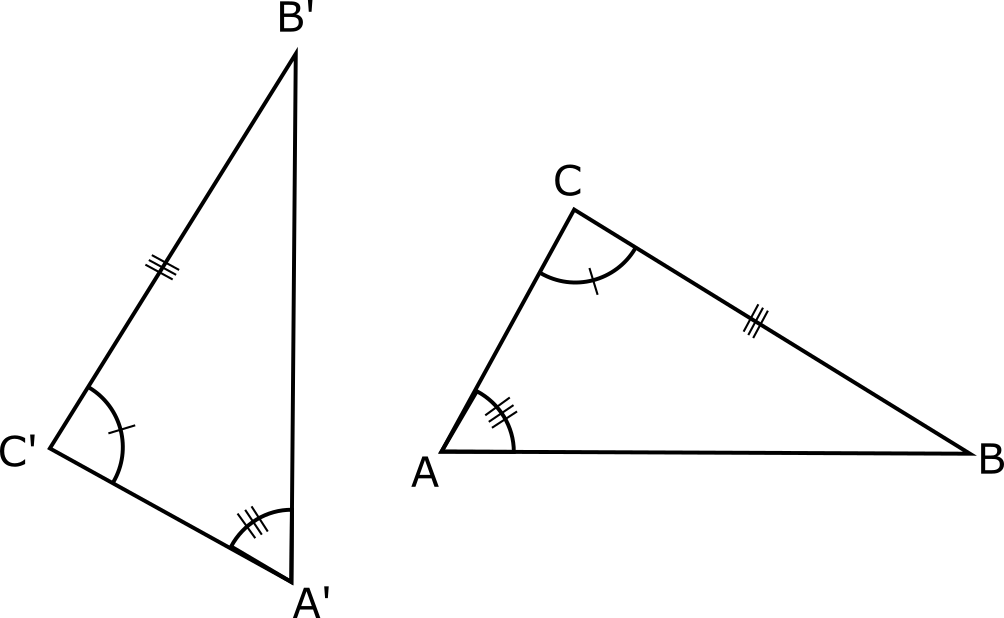
$$\triangle ABC \cong \triangle A'B'C'$$
$$\text{Sí y sólo si se cumplen las tres condiciones siguientes:}$$
$$ 4.~ \hat{A} \cong \hat{A'} $$
$$ 6.~ \hat{C} \cong \hat{C'} $$
$$ 2.~\overline{BC} \cong \overline{B'C'}~\text{opuestos a A y A', respectivamente}$$
5. CRITERIO RHC DE CONGRUENCIA DE TRIÁNGULOS RECTÁNGULOS
Dos triángulos rectángulos son congruentes si tienen respectivamente congruentes la hipotenusa y un cateto.
CONGRUENCIA DE LAS LÍNEAS NOTABLES HOMÓLOGAS
TEOREMA
Si dos triángulos son congruentes entonces las medianas, las alturas y las bisectrices respectivamente homólogas son congruentes.
PROPIEDADES DEL TRIÁNGULO ISÓSCELES
TEOREMA
- Un triángulo es isósceles si y sólo si tiene dos ángulos congruentes.
- En todo triángulo isósceles la mediana, la altura, la mediatriz (con respecto a su base) y la bisectriz del ángulo opuesto, coinciden y recíprocamente.
- Todo triángulo isósceles tiene respectivamente congruentes dos alturas, dos medianas y dos bisectrices.
DESIGUALDADES EN EL TRIÁNGULO
TEOREMA
Si un triángulo tiene dos lados no congruentes entonces al mayor de dichos lados se opone un ángulo mayor y recíprocamente.
COROLARIOS
- En todo triángulo rectángulo la hipotenusa es mayor que cada uno de los catetos.
- En todo triángulo obtusángulo el lado mayor es el que se opone al ángulo obtuso.
TEOREMA DE DESIGUALDAD TRIANGULAR
En todo triángulo cada lado es menor que la suma de los otros dos y mayor que el valor absoluto de la diferencia entre ellos.
COROLARIOS
- El camino más “corto” entre dos puntos es el segmento que los tiene por extremos.
- Toda poligonal abierta convexa es menor que cualesquiera otra poligonal abierta envolvente que tenga sus mismos extremos.
- Para que un triángulo exista dados sus tres lados, es suficiente que el lado mayor sea menor que la suma de los otros dos.
TEOREMA DE LA BISAGRA
Si dos triángulos tienen dos lados respectivamente congruentes y el ángulo comprendido desigual entonces al mayor ángulo comprendido se opone un mayor tercer lado y recíprocamente.
DISTANCIA DE UN PUNTO A UNA RECTA
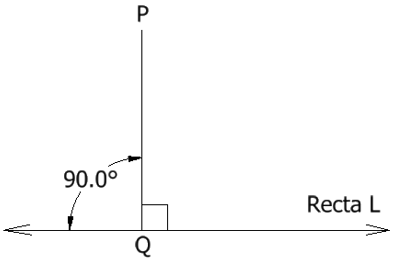
Se llama “distancia de un punto P a una recta L” a la mínima distancia entre el punto P y la recta L. Esta mínima distancia se da cuando se traza un segmento desde el punto P hasta un punto Q que pertenece a la recta L, tal que \(\overline{PQ} \perp \overleftrightarrow{L}\). Si el punto P es interior a la recta L entonces la distancia es cero.
La distancia de un punto a una semirrecta o a un segmento es la distancia del punto a la recta que contiene a la semirrecta o al segmento.
LUGAR GEOMÉTRICO (LG)
Una figura F es el lugar geométrico de una propiedad P si está formada por todos los puntos que cumplen la propiedad P y solamente por ellos.
1. TEOREMA DE LA MEDIATRIZ COMO LUGAR GEOMÉTRICO
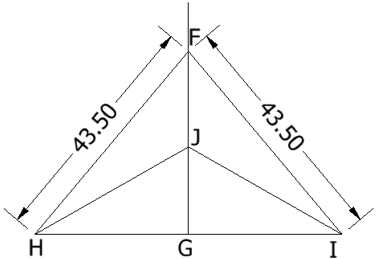
En un plano, la mediatriz de un segmento es el lugar geométrico de todos los puntos del plano que equidistan de los extremos del segmento. Así, en la figura siguiente, la mediatriz \(\overrightarrow{GF}\) es el lugar geométrico de todos los puntos del plano que equidistan de \(H\) e \(I\). Es decir, cualquier pareja de medidas de segmentos trazada desde estos dos puntos a cualquier punto sobre la mediatriz tendrá la misma medida. Por ejemplo, \(JH=JI\) o \(FH=FI\).
COROLARIO
En un plano, si dos puntos equidistan de los extremos de un segmento entonces la recta que ellos determinan es la mediatriz del segmento. Este corolario será muy útil para realizar la construcción de perpendiculares.
2. TEOREMA DE LA BISECTRIZ COMO LUGAR GEOMÉTRICO
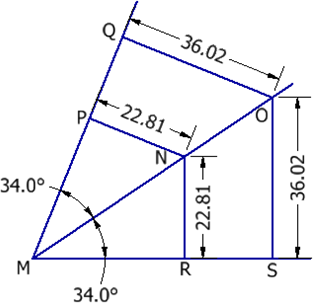
En un plano, la bisectriz de un ángulo es el lugar geométrico de los puntos del interior del ángulo que equidistan de los lados del ángulo. Así, en la figura siguiente, la bisectriz \(\overrightarrow{MO}\) es el lugar geométrico de los puntos que equidistan de los lados \(\overrightarrow{MQ}\) y \(\overrightarrow{MS}\). Debido a que la definición de distancia de un punto a una recta, semirrecta o segmento define que ésta debe medirse perpendicular a dicha recta, semirrecta o segmento, se tiene que \(\overline{OQ}\) y \(\overline{NP}\) son perpendiculares a \(\overrightarrow{MQ}\) y \(\overline{OS}\) y \(\overline{NR}\) son perpendiculares a \(\overrightarrow{MS}\). Finalmente, bajo esa condición, se tiene entonces que la bisectriz es lugar geométrico debido a que \(OQ=OS\), \(NP=NR\), y de igual manera para cualquier punto que se seleccione sobre la bisectriz \(\overrightarrow{MO}\).
COROLARIO
Si un punto del interior de un ángulo, equidista de los lados del ángulo, entonces pertenece a la bisectriz del ángulo.




Comentarios potenciados por CComment