SEGMENTOS
Recordemos que dados los puntos A y B, se llama segmento de recta AB (\(\overline{AB}\)) al conjunto formado por los puntos A, B y todos los puntos P entre A y B.
Los puntos A y B se llaman extremos. Las semirrectas determinadas por los extremos de un segmento y que no tienen más puntos comunes con el segmento, se llaman las prolongaciones del segmento.
MEDIDA DE SEGMENTOS: La medida de un segmento AB, denotada por \(m(\overline{AB})\) o AB, es la distancia entre sus puntos extremos:
$$ m(\overline{AB})=d(A,B)=AB $$
SEGMENTOS CONGRUENTES: Son segmentos que tienen igual medida:
$$ \overline{AB} \cong \overline{CD} \leftrightarrow m(\overline{AB})=m(\overline{CD}) \leftrightarrow AB=CD $$
CONVENCIÓN: Cuando no haya lugar a confusión en lugar de \( \overline{AB} \) usaremos AB y en lugar de \( \overline{AB} \cong \overline{CD} \) usaremos AB=CD.
SEGMENTOS DESIGUALES: Son segmentos no congruentes. Entre dos segmentos desiguales será menor el que tenga menor medida:
$$ \overline{AB} < \overline{CD} \leftrightarrow m(\overline{AB})<m(\overline{CD}) \leftrightarrow AB<CD $$
AXIOMA DE CONSTRUCCIÓN DE SEGMENTOS: En toda semirrecta \( \overrightarrow{OA} \), para cada real positivo ''x'', existe un único punto B sobre \( \overrightarrow{OA} \), distinto de O, tal que \( m(\overline{OB})=x \).
PUNTO MEDIO DE UN SEGMENTO: Es el punto entre los extremos del segmento que lo divide en dos segmentos congruentes.
| M es punto medio de \( \overline{AB} \leftrightarrow \overline{AM} \cong \overline{MB}\) |
ó
| M es punto medio de \( \overline{AB} \leftrightarrow AM = MB = AB/2 \) |
SEGMENTOS ADYACENTES: Son dos segmentos de extremos colineales y que tienen un extremo común situado entre los extremos no comunes.
SUMA DE SEGMENTOS: Si \( \overline{AB} \) y \( \overline{BC} \) son segmentos adyacentes entonces el segmento \( \overline{AC} \) es la suma de los segmentos \( \overline{AB} \) y \( \overline{BC} \):
$$ AC=AB+BC $$
Además:
$$ AB=AC-BC $$
$$ BC=AC-AB $$
Para sumar dos segmentos no adyacentes se construyen dos segmentos adyacentes respectivamente congruentes a ellos.
ÁNGULOS
ÁNGULO: Es la figura formada por dos semirrectas que tienen el mismo origen. Si ellas son \( \overrightarrow{OA} \) y \( \overrightarrow{OB} \), se denota por \( \angle AOB \) o \( A\hat{O}B \). El origen O es el vértice del ángulo y las semirrectas son los lados del ángulo.

INTERIOR DE UN ÁNGULO: Es el conjunto formado por los puntos que están en la intersección de dos semiplanos, (cada uno de ellos con un lado sobre su borde y conteniendo al lado restante), excepto los que están sobre los lados del ángulo.
EXTERIOR DE UN ÁNGULO: Es el subconjunto del plano del ángulo formado por los puntos que no están sobre los lados del ángulo ni en el interior del ángulo.
ÁNGULO NULO: Es el ángulo que forma toda semirrecta consigo misma.
ÁNGULO LLANO: Es el ángulo formado por dos semirrectas opuestas.
AXIOMA DE MEDIDA DE ÁNGULOS: Dado un semiplano con una semirrecta \( \overrightarrow{OA} \), fija en su borde, entonces a cada semirrecta de dicho semiplano, se le asigna un único número real ''a'' en el intervalo [0,180]. Para la semirrecta \( \overrightarrow{OA} \) se asigna el 0 y para su semirrecta opuesta el 180.
MEDIDA SEXAGESIMAL DE UN ÁNGULO: La ''medida'' (sexagesimal) de un \( \angle AOB\) es igual a ''a'' grados sexagesimales, tomando el número real ''a'' en el intervalo [0,180], que le asigna el axioma anterior y lo denotaremos por:
$$ m( \angle AOB)=a $$
O simplemente:
$$ \angle AOB=a $$
CLASIFICACIÓN SEGÚN SU MEDIDA:
Según su medida los ángulos se clasifican así:
- \( \alpha \) es NULO si \( \alpha=0° \).
- \( \alpha \) es AGUDO si \( 0° < \alpha < 90° \).
- \( \alpha \) es RECTO si \( \alpha=90° \).
- \( \alpha \) es OBTUSO si \( 90° < \alpha < 180° \).
- \( \alpha \) es LLANO si \( \alpha =180° \).
ÁNGULOS CONGRUENTES: Son ángulos que tienen igual medida:
$$ \angle ABC \cong \angle DEF \leftrightarrow m(\angle ABC)=m( \angle DEF) $$
CONVENCIÓN: Cuando no haya lugar a confusión en lugar de \( \angle ABC \cong \angle DEF \) o de \( m(\angle ABC)=m( \angle DEF) \) usaremos \( \angle ABC= \angle DEF \).
ÁNGULOS DESIGUALES: Son dos ángulos no congruentes. Entre dos ángulos desiguales será menor el que tenga menor medida.
AXIOMA DE CONSTRUCCIÓN DE ÁNGULOS: Dado un semiplano y fijada una semirrecta \( \overrightarrow{OA} \) sobre su borde, entonces para cada real ''x'' en el intervalo [0,180], existe solamente una semirrecta \( \overrightarrow{OB} \) en dicho semiplano, tal que \( m( \angle AOB ) = x° \).
BISECTRIZ DE UN ÁNGULO: Es la semirrecta interior que lo divide en dos ángulos congruentes. Si \( \overrightarrow{BX} \) es una la semirrecta interior al \( \angle ABC \) entonces:
| \( \overleftrightarrow{BX} \) es bisectriz de \(\angle ABC \leftrightarrow \angle ABX = \angle XBC = \angle ABC/2 \) |

ÁNGULOS ADYACENTES: Son dos ángulos coplanares que tienen el mismo vértice, un lado común y cada uno de los lados no comunes está en el exterior del otro ángulo.

SUMA DE ÁNGULOS: Si \( \angle AOC \) y \( \angle COB \) son adyacentes, entonces el \( \angle AOB \) es la suma de los ángulos \( \angle AOC \) y \( \angle COB \):
$$ \angle AOB = \angle AOC + \angle COB $$
Además:
$$ \angle AOC = \angle AOB - \angle COB $$
$$ \angle COB = \angle AOB - \angle AOC $$
Para sumar dos ángulos no adyacentes se construyen dos ángulos adyacentes respectivamente congruentes a ellos.
ÁNGULOS COMPLEMENTARIOS: Son dos ángulos cuyas medidas suman 90°. De cada uno de ellos se dice que es el complemento del otro:
$$ \angle A + \angle B = 90° $$
ÁNGULOS SUPLEMENTARIOS: Son dos ángulos cuyas medidas suman 180°. Cada uno de ellos es el suplemento del otro:
$$ \angle A + \angle B = 180° $$
PAR LINEAL: Son dos ángulos adyacentes cuyos lados no comunes son semirrectas opuestas.
ÁNGULOS OPUESTOS POR EL VÉRTICE: Son dos ángulos tales que los lados de uno de ellos son las semirrectas opuestas de los lados del otro.
TEOREMA: Si dos ángulos forman un par lineal entonces son suplementarios.
TEOREMA: Si dos ángulos adyacentes, \( \angle ABC \) y \( \angle CBD \) son suplementarios entonces forman un par lineal y por lo tanto los puntos A, B y D son colineales.
** Este teorema se utilizará para probar que tres puntos son colineales.
TEOREMA DE ÁNGULOS OPUESTOS POR EL VÉRTICE: Dos ángulos opuestos por el vértice son congruentes.
TEOREMA: Las bisectrices de dos ángulos opuestos por el vértice son semirrectas opuestas.
RECTAS PERPENDICULARES: Dos rectas secantes L y M son perpendiculares, \( L \perp M\), si forman por lo menos un ángulo recto. En caso contrario son oblicuas.

Dos segmentos (semirrectas) son perpendiculares si están contenidos en rectas perpendiculares.
TEOREMA: Dos rectas perpendiculares forman cuatro ángulos rectos.
TEOREMA: Las bisectrices de un par lineal son perpendiculares.
TEOREMA: Por cada punto de una recta pasa una y solamente una recta perpendicular a ella.
Demostración: Por el axioma de construcción de ángulos para x=90 existe una y sólo una semirrecta que determina la recta pedida.
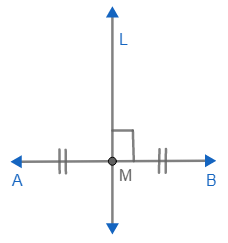
MEDIATRIZ DE UN SEGMENTO: Es la recta que pasa por el punto medio de un segmento y es perpendicular al segmento.
Si M es el punto medio de \( \overline{AB} \) y \( \overleftrightarrow{L} \perp \overline{AB}\) entonces \(\overleftrightarrow{L}\) es mediatriz de \( \overline{AB} \):
LÍNEA POLIGONAL: Sea \(n \in Z^+ \) y \( n \geq 3 \). Si \(A_1, A_2, ... , An\) son puntos coplanares, tales que ninguna tripleta de consecutivos son colineales entonces a la unión de los segmentos \( \overline{A_1 A_2}, \overline{A_2 A_3}, ... , \overline{A_{n-1} A_n} \) se le llama poligonal \(A_1 A_2 ... A_n\).
Los extremos de cada segmento son los vértices de la poligonal, los segmentos son los lados y la suma de las medidas de sus lados es el perímetro.
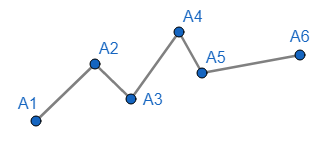
Si el extremo final del último segmento coincide con el inicial del primero entonces la poligonal es cerrada, en caso contrario la poligonal es abierta.
POLÍGONO: Es la región del plano limitada por una poligonal cerrada. Según el número de lados se llaman:
- Triángulo (3).
- Cuadrilátero (4).
- Pentágono (5).
- Hexágono (6).
- Heptágono (7).
- Octágono (8).
- Eneágono (9).
- Decágono (10).
- Dodecágono (12).
- Pentedecágono (15).
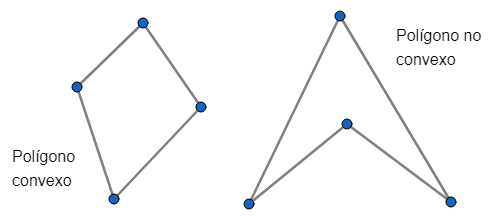
POLÍGONO CONVEXO: Un polígono es convexo si al unir dos puntos cualesquiera situados sobre dos lados distintos, el segmento está contenido en el polígono. En caso contrario es no convexo.
ÁNGULO INTERIOR DE UN POLÍGONO: ángulo interior de un polígono convexo es el formado por dos lados consecutivos.
ÁNGULO EXTERIOR DE UN POLÍGONO: ángulo exterior es el que forma un par lineal con un ángulo interior.
POLÍGONO REGULAR: Es un polígono con todos sus lados congruentes y todos sus ángulos interiores congruentes.
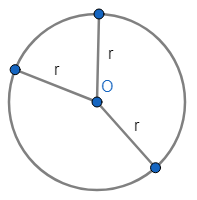
CIRCUNFERENCIA: Dados un plano \( \pi \), un punto O en dicho plano, y un número real positivo r, (r > 0), se llama ''Circunferencia de centro O y radio r en el plano \( \pi \)'' y se denota por: ''C(O;r)'', al conjunto formado por todos los puntos P del plano \( \pi \) tales que su distancia al centro es igual a r, es decir, tales que OP = r.




Comentarios potenciados por CComment