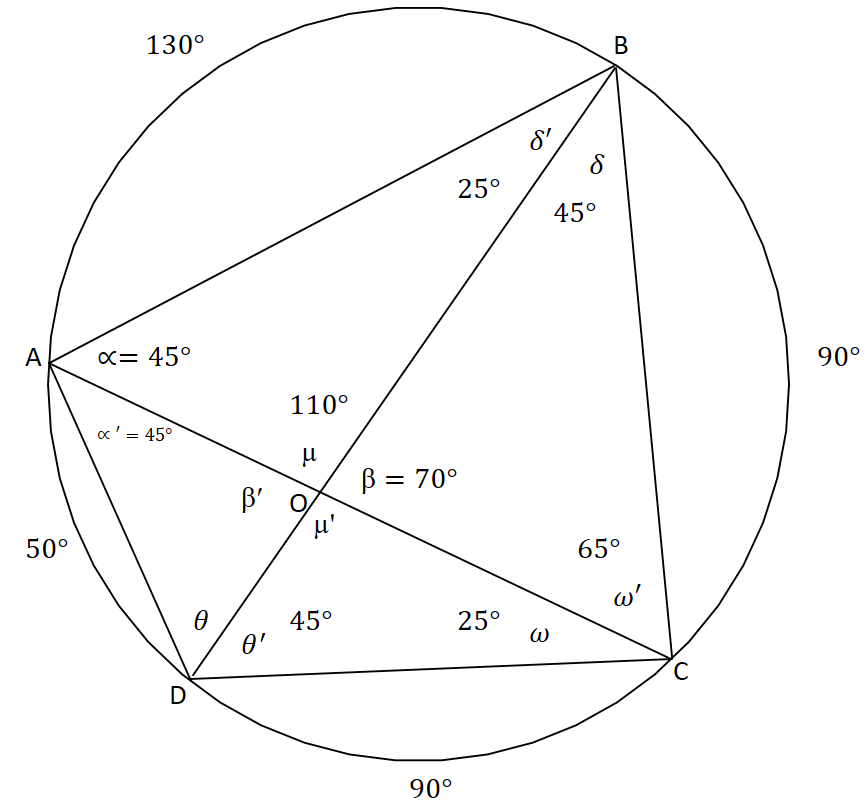
21. Encontrar los ángulos de un cuadrilátero inscriptible ABCD, si AC forma con los lados AB y AD ángulos de 45° y con BD un ángulo de 70° (tome el ángulo BOC=70°, con O punto de intersección entre AC y BD).
DESARROLLO
HIPÓTESIS
1. Circunferencia centro en P y radio r: C(P,r).
2. ABCD cuadrilátero inscriptible (los vértices pertenecen a la circunferencia).
3. \( m(B\hat{A}C) = \alpha = 45° \).
4. \( m(C\hat{A}D) = \alpha ' = 45° \).
5. \( m(B\hat{O}C) = \beta = 70° \).
TESIS
\( m(B\hat{A}D) = ? \).
\( m(A\hat{D}C) = ? \).
\( m(D\hat{C}B) = ? \).
\( m(C\hat{B}A) = ? \).
| PROPOSICIÓN | RAZÓN | |
| 6. | $$ \theta'=45° $$ | Corolario del Teorema del Ángulo Inscrito. Todos los ángulos inscritos que subtienden el mismo arco (BC) son congruentes. |
| 7. | $$ \delta=45° $$ | Corolario del Teorema del Ángulo Inscrito. Todos los ángulos inscritos que subtienden el mismo arco (DC) son congruentes. |
| 8. | $$ m(\overset{\frown}{BC})=90° $$ | Por el Teorema del ángulo inscrito. De 3. |
| 9. | $$ m(\overset{\frown}{DC})=90° $$ | Por el Teorema del ángulo inscrito. De 4. |
| 10. | $$ \beta=\beta'=70° $$ | Por Teorema de ángulos opuestos por el vértice y 5. |
| 11. | $$ m(\overset{\frown}{AD})=50° $$ | Por Teorema del ángulo interior aplicado a \(\beta\) usando 8. |
| 12. | $$ \omega=25° $$ | Por Teorema del ángulo inscrito usando valor del arco AD. De 11. |
| 13. | $$ \delta'=25° $$ | Por Teorema del ángulo inscrito usando valor del arco AD. De 11. |
| 14. | $$ \mu=180°-\beta=110° $$ | Por axioma de medida de ángulos usando valor de \(\beta\). De 10. |
| 15. | $$\overset{\frown}{AB}=360°-\overset{\frown}{AD}-\overset{\frown}{DC}-\overset{\frown}{BC} = 130° $$ | Por axioma de medida de arcos y diferencia de arcos usando 8, 9, 11 y propiedades de los reales. |
| 16. | $$ \theta=\omega'=65° $$ | Por Teorema de ángulo inscrito usando valor del arco AB. De 15. |
| 17. | $$ m(B\hat{A}D) = \alpha+\alpha' = 90° $$ | Por suma de ángulos adyacentes. Suma de 3 y 4. |
| 18. | $$ m(A\hat{D}C) = \theta+\theta' = 110° $$ | Por suma de ángulos adyacentes. Suma de 6 y 16. |
| 19. | $$ m(D\hat{C}B) = \omega+\omega' = 90° $$ | Por suma de ángulos adyacentes. Suma de 12 y 16. |
| 20. | $$ m(C\hat{B}A) = \delta+\delta' = 70° $$ | Por suma de ángulos adyacentes. Suma de 7 y 13. |





Comentarios potenciados por CComment