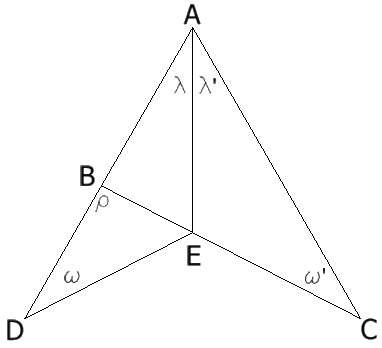
En un triángulo \(\triangle ABC\) con AB<AC, se traza la bisectriz \(\overline{AE}\). Se prolonga \(\overline{AB}\) hasta D, tal que AD=AC, y se traza \(\overline{DE}\). Probar que BE<EC.
Hipótesis
\(\triangle ABC\)
AB<AC
\(\overline{AE}\) bisectriz de \(B\hat{A}C\)
\(\overline{BD}\) prolongación de \(\overline{AB}\)
AD=AC
Tesis
BE<EC
| Proposición | Razón | |
| 1. | Hipótesis. | Por hipótesis. |
| 2. | AE=AE | Propiedad de los reales (reflexiva). |
| 3. | \(\lambda = \lambda'\) | \(\overline{AE}\) es bisectriz. Por hipótesis. Por definición de bisectriz de un ángulo. |
| 4. | AD=AC | Por hipótesis. |
| 5. | \(\triangle AEC \cong \triangle AED\) | Criterio LAL (Lado Ángulo Lado). De 2, 3 y 4. |
| 6. | DE=EC | Lados Homólogos (o correspondientes) en triángulos congruentes. De 5. |
| 7. | \(\omega = \omega'\) | Ángulos Homólogos (o correspondientes) en triángulos congruentes. De 5. |
| 8. | \(\rho>\omega'\) | Teorema de ángulo exterior de un triángulo en desigualdades: un ángulo exterior es mayor que cualquiera de los ángulos interiores no adyacentes. Aplica para \(\triangle ABC\). |
| 9. | \(\rho>\omega\) | Sustitución de 7 en 8. |
| 10. | DE>BE | Teorema de desigualdad AL (ángulo --> lado). De 9. |
| 11. | EC>BE v BE<EC | Sustitución de 6 en 10. |




Comentarios potenciados por CComment