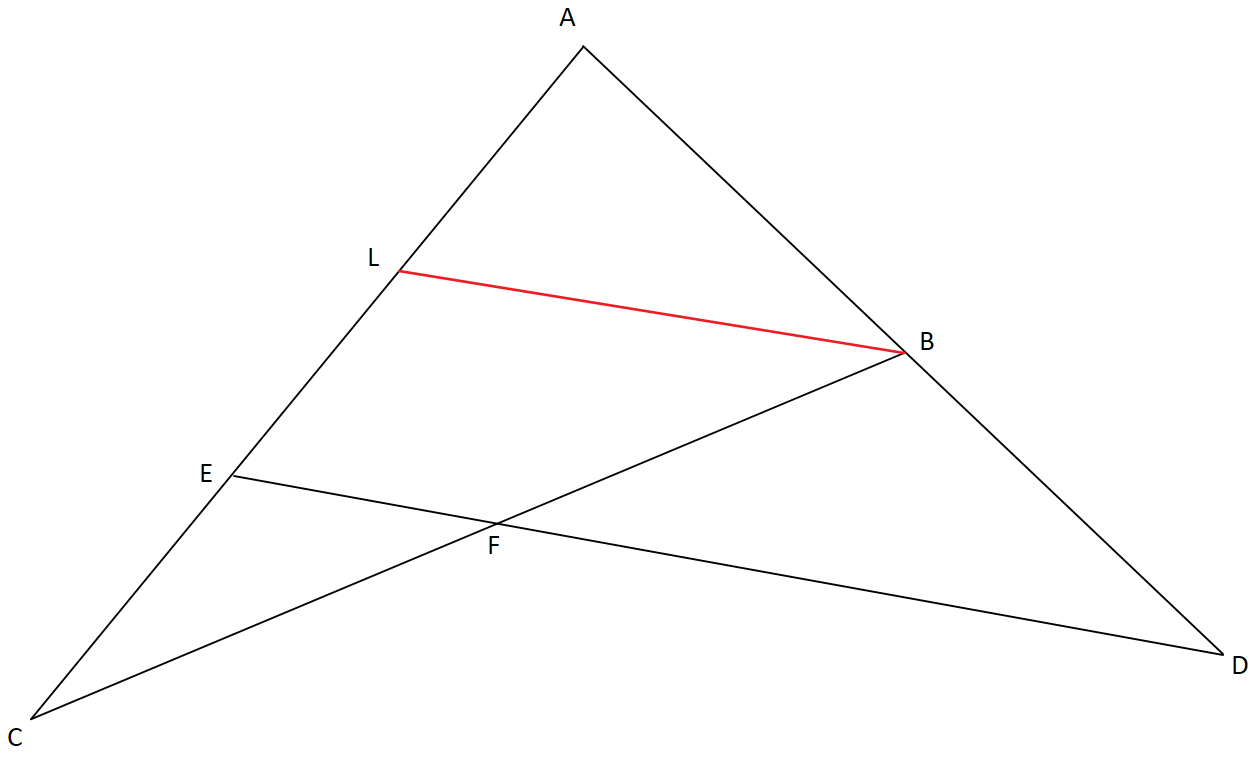
Ejercicio 11 | Geometría Euclidiana | Semejanza | Recíproco del teorema de la base media

Visto: 18255

11. Se tiene el triángulo ABC. Sean A-B-D, tales que AB=BD. Sean A-E-C tales que (AE/EC)=(3/2). Los segmentos DE y BC se cortan en F. Hallar BF/BC.

DESARROLLO

HIPÓTESIS

1. △ABC cualquiera.

2. A−B−D.

3. AB=BD.

4. A−E−C.

5. AE/EC=3/2.

6. ¯DE∩¯BC=F.

TESIS

Hallar razón BF/BC.

PROPOSICIÓN RAZÓN
7. Trazo BL con A-L-E-C y ¯BL∥¯DE∥¯FE. Construcción auxiliar.
8. B es punto medio de AD. Por definición de punto medio de un segmento. De 3.
9. L es punto medio de segmento AE. Por el recíproco del Teorema de la base media de un triángulo (△ADE), que dice: si trazo un segmento desde el punto medio del lado de un triángulo paralelo a otro lado del mismo triángulo, entonces el punto de intersección será punto medio de su respectivo lado. De 7 y 8.
10. BFBC=LELC Por el Teorema Fundamental de Segmentos Proporcionales. Se tienen las paralelas FE y BL. De 7.
11. LE=AE2 De 9. Por definición de punto medio de un segmento.
12. AE=32EC De 5. Propiedad de las proporciones.
13. LE=34EC Sustitución de 12 en 11.
14. LC=LE+EC Suma de segmentos adyacentes.
15. EC=44EC Propiedad de los reales.
16. LC=(3/4)EC+(4/4)EC Sustitución de 13 y 15 en 14.
17. LC=74EC De 16. Propiedad de los reales.
18. BFBC=(3/4)EC(7/4)EC Sustitución de 13 y 17 en 10.
19. BFBC=37 De 18. Propiedad de los reales.

Comentarios (0)

    Attach images by dragging & dropping or by selecting them.
    The maximum file size for uploads is 5MB. Only gif,jpg,png files are allowed.
     
    The maximum number of 3 allowed files to upload has been reached. If you want to upload more files you have to delete one of the existing uploaded files first.
    The maximum number of 3 allowed files to upload has been reached. If you want to upload more files you have to delete one of the existing uploaded files first.
    Comentando como

    Comentarios potenciados por CComment