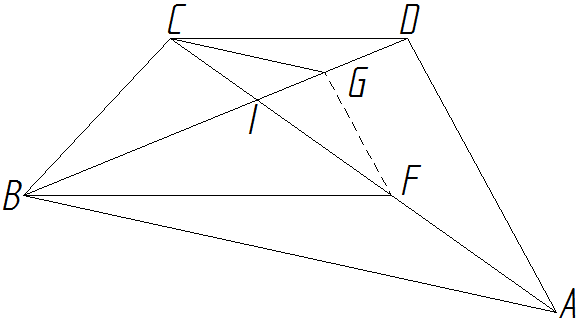
En un cuadrilátero ABCD se traza por B, BF paralela a CD (F sobre la diagonal AC) y por C, CG paralela a AB (G sobre la diagonal BD). Demostrar que FG es paralela a AD.

Hipótesis:
ABCD cuadrilátero cualquiera.
$\overline{BF} \parallel \overline{CD}$
$\overline{CG} \parallel \overline{AB}$
$F \in \overline{AC}$.
$G \in \overline{BD}$.

Tesis:
$\overline{FG} \parallel \overline{AD}$.

Proposición - Razón

1. $\frac{DI}{IB}=\frac{CI}{IF}$ Por Teorema fundamental de proporcionalidad.

$$\frac{CI}{IA}=\frac{GI}{IB}$

2. $DI.IF=CI.IB$ Por propiedad de proporciones.

$GI.IA=CI.IB$

3. $DI.IF=GI.IA$ Por transitividad entre 2a y 2b.

4. $\frac{GI}{DI}=\frac{IF}{IA}$ Por propiedad de proporciones.

5. $DI=GI+GD$ Por suma de segmentos.

$IA=IF+FA$

6. $\frac{GI}{GI+GD}=\frac{IF}{IF+FA}$ Por sustitución de 5a y 5b en 4.

7. $\frac{GI+GD}{GI}=\frac{IF}{IF+FA}$ Por propiedad de proporciones.

8. $\frac{GI}{GI}+\frac{GD}{GI}=\frac{IF}{IF}+\frac{FA}{IF}$ Por propiedad de los reales.

9. $1+\frac{GD}{GI}=1+\frac{FA}{IF}$ Por propiedad de los reales (cancelativa), de 8.

10. $\frac{GD}{GI}=\frac{FA}{IF}$ Por propiedad de los reales.

11. $\overline{FG} \parallel \overline{AD}$ Por sexto criterio de paralelismo.