Geometría Euclidiana | Proporcionalidad | Ejercicio resuelto | Ej. 6
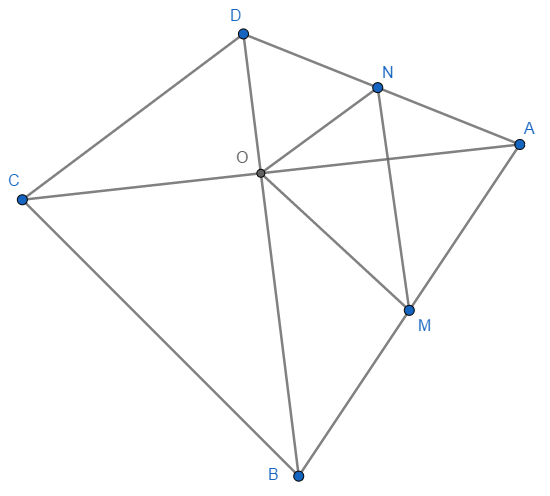
ABCD es un cuadrilátero cualquiera cuyas diagonales se cortan en O. Por O se traza \(\overline{OM} \parallel \overline{BC}\), cortando a \(\overline{AB}\) en M. Sea N un punto en \(\overline{AD}\) tal que \(\overline{MN} \parallel \overline{BD}\). Demostrar que \(\overline{ON} \parallel \overline{CD}\).
Hipótesis:
1. ABCD cuadrilátero cualquiera.
2. \(\overline{AC} \cap \overline{BD} = {O}\).
3. A-M-B.
4. \(\overline{OM} \parallel \overline{BC}\).
5. A-N-D.
6. \(\overline{MN} \parallel \overline{BD}\)
Tesis:
\(\overline{ON} \parallel \overline{CD}\)
Demostración
| 7. $$ \frac{AM}{MB}=\frac{AO}{OC} $$ | De 4. Por el teorema fundamental de segmentos proporcionales (TFSP). |
| 8. $$ \frac{AM}{MB}=\frac{AN}{ND} $$ | De 6. Por el TFSP. |
| 9. $$ \frac{AO}{OC}=\frac{AN}{ND} $$ | Por transitividad (propiedad transitiva) entre los pasos 7 y 8. |
| 10. \(\overline{ON} \parallel \overline{CD}\). | Por criterio de paralelismo (recíproco del TFSP): si en un triángulo una recta determina segmentos proporcionales sobre dos lados (o sobre sus prolongaciones) entonces dicha recta es paralela al tercer lado. |




Comentarios potenciados por CComment