Ejercicio 8 | Geometría Euclidiana | Semejanza | Teorema de razón entre líneas notables

Visto: 1183

8. En un triángulo rectángulo ABC de hipotenusa a y altura h, se inscribe un cuadrado que tiene un lado sobre la hipotenusa. Calcular el lado del cuadrado en función de a y h.

SOLUCIÓN

HIPÓTESIS

1. \( \triangle ABC \) rectángulo.

2. Hipotenusa \( BC=a \).

3. Altura \( AH=h \) del triángulo \( ABC \).

4. Cuadrado FGED de lado \( l \) inscrito en \(\triangle ABC\). Lado DE pertenece a la hipotenusa.

TESIS

\( l=f(a,h) \).

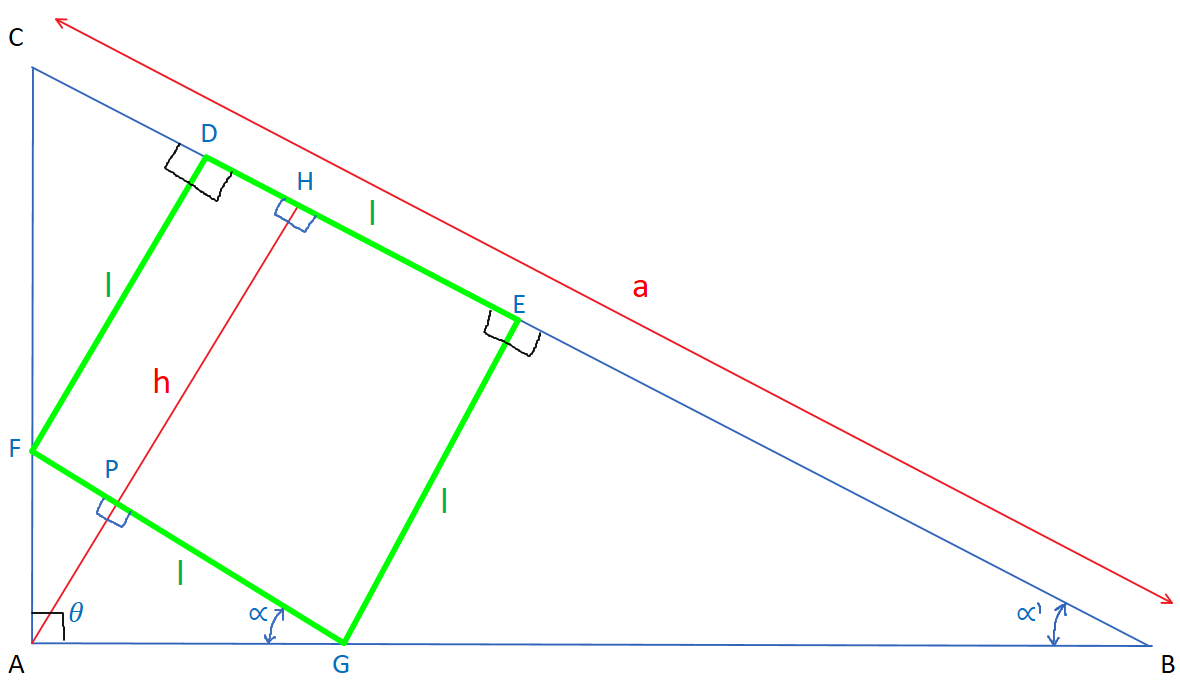
PROPOSICIÓN RAZÓN
5. $$ m(C\hat{A}B)=\theta=90° $$ De 1. Por definición de triángulo ABC rectángulo.
6. $$ FG \parallel CB $$ De 4. Lado DE pertenece a la hipotenusa CB, luego C-D-E-B son colineales. FG es paralelo con CB por propiedad del cuadrado. Sus lados opuestos son paralelos.
7. $$ \alpha = \alpha' $$ De 6. Se tienen dos paralelas y una transversal que es la recta B-G-A. Con esto, se puede usar el Teorema de ángulos correspondientes congruentes que se forman entre dos paralelas y una transversal.
8. $$ \triangle FAG \sim \triangle ABC $$ Por el criterio de Semejanza Ángulo-Ángulo (SAA). Los ángulos congruentes se tienen en los pasos 5 (común a ambos triángulos) y 7.
9. $$ AH \perp CB $$ De 3. Por la definición de altura del triángulo ABC.
10. $$ AP \perp FG $$ Por criterio de perpendicularidad, que dice: si tengo dos rectas paralelas, toda perpendicular a una de ellas, será también perpendicular a la otra. El paralelismo está dado en 6 y la perpendicularidad está dada en 9.
11. \( AP \) es una altura del triángulo FAG. Por la definición de altura. De 10.
12. $$ \frac{FG}{CB}=\frac{AP}{AH} $$ Por el teorema que dice: si dos triángulos son semejantes, entonces la razón entre dos elementos rectilíneos homólogos (alturas, medianas, bisectrices) es igual a la razón de semejanza entre los triángulos. Semejanza demostrada en 8. Elementos homólogos demostrados en 3 y 11.
13. $$ \frac{l}{a}=\frac{AP}{h} $$ Por sustitución de 2, 3 y 4 en 12.
14. $$ l = \frac{a . AP}{h} $$ De 13. Propiedad de las proporciones.
15. $$ GE \perp DE $$ Por definición de cuadrado. De 4.
16. $$ PH \perp DE $$ De 9. PH pertenece a AH y DE pertenece a CB.
17. $$ GE \parallel PH $$ Por criterio de paralelismo que dice: dos rectas que son perpendiculares a una tercera, son paralelas. De 15 y 16.
18. Cuadrilátero HEGP es un paralelogramo. Por la definición de paralelogramo: cuadrilátero con ambos pares de lados opuestos paralelos. De 6 y 17.
19. $$ PH=GE $$ Por propiedad de los paralelogramos. Lados opuestos congruentes. De 18.
20. $$ AP = AH - PH $$ Diferencia de segmentos.
21. $$ AP = h - GE $$ Sustitución de 3 y 19 en 20.
22. $$ AP = h - l $$ Sustitución de 4 en 21.
23. $$ l = \frac{a . (h-l)}{h} $$ Sustitución de 22 en 14.
24. $$ l = \frac{a.h}{h+a} $$ De 23. Propiedad de los reales.

Comentarios potenciados por CComment