A continuación se demostrará el teorema de Pitágoras demostrando primero que el cateto de un triángulo rectángulo es media proporcional, al igual que la altura relativa a la hipotenusa.

Hipótesis:
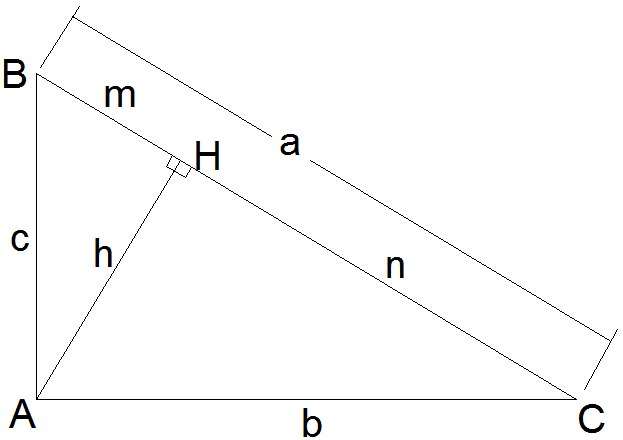
\(\triangle ABC\) rectángulo en A. \(\overline{AH}\) altura relativa a la hipotenusa.

Tesis:
\(b^2=a \cdot n\).

\(c^2=a \cdot m\).

\(h^2=m \cdot n\).

\(a^2=b^2+c^2\)

Proposición - Razón

1. \(\triangle CHA \sim \triangle ABC\) y \(\triangle AHB \sim \triangle ABC\). Por teorema de altura relativa a la hipotenusa (semejanza).

2. \(\frac{a}{b}=\frac{b}{n}=\frac{c}{h}~~~\text{y}~~~\frac{a}{c}=\frac{c}{m}=\frac{b}{h}\). Por propiedad de semejanza de triángulos entre \(\triangle CHA\) y \(\triangle ABC\) y entre \(\triangle AHB\) y \(\triangle ABC\). De 1.

3. \(b^2=a \cdot n~~~\text{y}~~~c^2=a \cdot m\). Por propiedad de las proporciones. De 2.

4. \(\triangle CHA \sim \triangle AHB\) Por teorema de altura relativa a la hipotenusa (semejanza).

5. \(\frac{n}{h}=\frac{h}{m}=\frac{b}{c}\) Por propiedad de semejanza entre \(\triangle CHA\) y \(\triangle AHB\).

6. \(h^2=m \cdot n\) Por propiedad de las proporciones. De 5.

7. \(b^2 + c^2 = a \cdot n + a \cdot m\) Por suma de 3a y 3b.

8. \(b^2 + c^2 = a (n + m)\) Por propiedad de los reales. De 7.

9. \(b^2 + c^2 = a \cdot a\) Por sustitución de \((a=n+m)\) en 8.

10. \(a^2=b^2 + c^2\) Por propiedad de los reales. De 9.